Es sei S 1 = x y ∈ R 2 : x 2 + y 2 = 1 der Einheitskreis im R 2 .
Konstruieren Sie Geraden G1, G2 G3 mit den folgenden Eigenschaften. Weisen Sie jeweils nach, dass die von ihnen angegebenen Geraden die geforderten Eigenschaften haben.
(1) Geben Sie eine Gerade G1 an, so dass G1 ∩ S 1 = ∅ gilt.
(2) Geben Sie eine Gerade G2 an, so dass G2 ∩ S 1 aus genau einem Punkt besteht.
(3) Geben Sie eine Gerade G3 an, so dass G3 ∩ S 1 aus genau zwei Punkten besteht. Bestimmen Sie außerdem ai , bi , ci ∈ R, so dass Gi = x y ∈ R : aix + biy = ci gilt.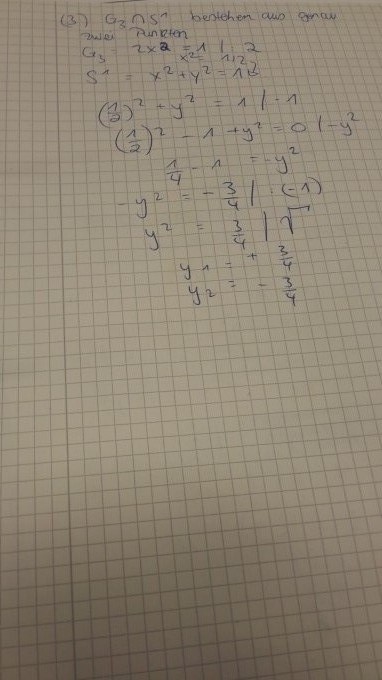

Ich habe die Aufgabe von crazymath aus Neugier versuchen zu lösen,da darauf nicht geantwortet wurde und würde gerne wissen, ob ich die Aufgabe richtig gelöst habe ? Bei 2) weiß ich 100%dass ich irgendetwas falsch gemacht habe ..
Und wie bestimmt man Gi?