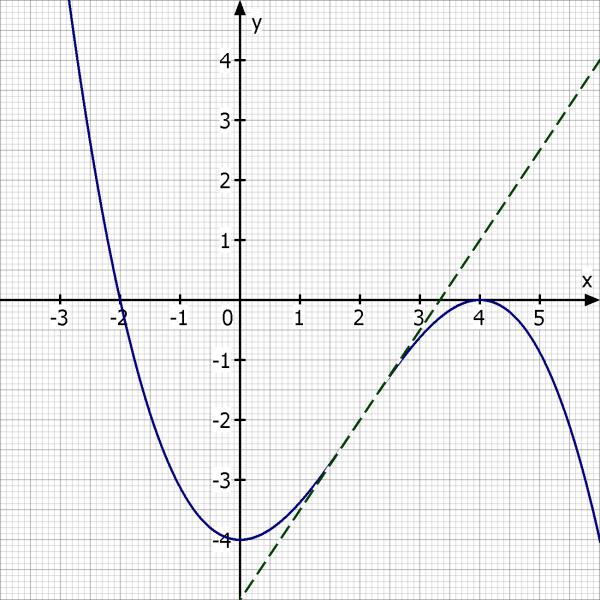
f(x) = - 1/8·x^3 + 3/4·x^2 - 4
f'(x) = 3/2·x - 3/8·x^2
f''(x) = 3/2 - 3/4·x
Wendestelle f''(x) = 0
3/2 - 3/4·x = 0
x = 2
Wendetangente
t(x) = f'(2) * (x - 2) + f(2) = 3/2 * (x - 2) - 2 = 3/2·x - 5
Diese Funktion kann man jetzt noch in die Koordinatenform bringen. Das muss man aber normalerweise nicht, wenn es in der Aufgabe nicht steht.
y = 3/2·x - 5
3/2·x - y = 5
3·x - 2·y = 10
Nullstelle der Wendetangente t(x) = 0
3/2·x - 5 = 0
x = 10/3
Winkel der Wendetangente mit der x-Achse
arctan(3/2) = 56.31°
Der Winkel ist also 56.31°
Skizze: