Nullstellen der Funktion f auf zwei Nachkommastellen genau berechnen

Question

Gegeben ist folgende Funktion: f(x)=ln(x⁴+5x³-5)

So bin ich vorgegangen:

Nullstelle finden heißt: f(x)=0 ⇒ ln(x⁴+5x³-5)=0

ln(y)=0  wenn y=0, also muss x⁴+5x³-5=0

Faktorisierung: x⁴+5x³-5 = (x-1)*(x³+6x²+6x+6) = 0

daraus weiß ich das x=1 eine Nullstelle ist.

Newton-Verfahren: $$ { x }_{ n+1 }\quad =\quad { x }_{ n }\quad -\quad \frac { f({ x }_{ n }) }{ f'({ x }_{ n }) } \\ { x }_{ n+1 }\quad =\quad { x }_{ n }\quad -\quad \frac { { { { x }_{ n } }^{ 4 }+5{ { x }_{ n } }^{ 3 }-6 } }{ 4{ { x }_{ n } }^{ 3 }+15{ x }_{ n }^{ 2 } } \\ $$

Startwert: x₀=-6 

x₁=...= -5,35185

x2=...=-5,09066 das ist die Nullstelle auf zwei Nachkommastellen genau.

Wie komme ich zu den fehlenden zwei Nullstellen, diese sind komplexe Nullstellen.?

Stimmt meine Vorgangsweise?

Answer 1

LN(x^4 + 5·x^3 - 5) = 0

x^4 + 5·x^3 - 5 = 1
x^4 + 5·x^3 - 6 = 0

Nullstelle gefunden bei x = 1

(x^4 + 5·x^3 - 6) : (x - 1) = x^3 + 6·x^2 + 6·x + 6

Ich habe als reelle Nullstelle

x = -5.046680324

Für die komplexen Nullstellen schaue unter:

http://www.arndt-bruenner.de/mathe/scripts/polynome.htm

Answer 2

ln(y)=0  wenn y=0 FALSCH!

wenn y=1, denn log(1)=0 oder per Umkehrfunktion e^0 =1

Die Gleichung x⁴ + 5·x³ - 6 = 0 

hat 4 Lösungen.

Lösungsweg 1 kommt zuerst in der Schule dran & wurde von Mathecoach bereits beschrieben.

Die Nullstellenfunktion für die Newton-Iteration (siehe

http://www.gerdlamprecht.de/Roemisch_JAVA.htm#ZZZZZ0118

) lautet pow(x,3)+6*x*x+6*x+6 bei Startwert aB[0]=-5 ist man schon nach 1 Schritt auf 2 Stellen genau.

Aber wenn man schon iteriert (numerisch antastet), kann man auch gleich die Originalfunktion nehmen:

Lösungsweg2

pow(x,4)+5*pow(x,3)-6

http://www.gerdlamprecht.de/Roemisch_JAVA.htm#@Px,4)+5*@Px,3)-6@Na=0;@B0]=-5;//Startwert@Nb=@Bi];a=@Bi+1]=b-Fx(b)/@Lb);@N@Aa-b)%3C4e-8@N1@N0@N#

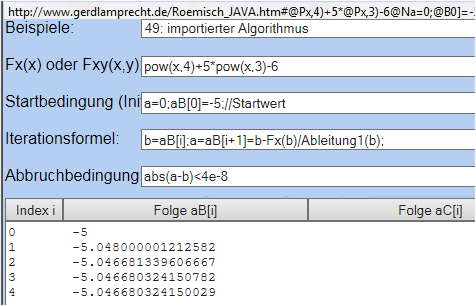
andere (Einschwing-)Lösung für Startwert im Bereich aB[0]=-0.5 bis aB[0]=5

ergibt immer 1.

Lösungsweg 3

Analog zur pq-Formel (quadratische Lösung), gibt es bei Polynomen von Grad 3 & Grad 4 fertige explizite PQRSTUVW-Formeln, die man nur einsetzen braucht, was http://www.lamprechts.de/gerd/php/gleichung-6-grades.php

online vorrechnet:

Das ist aber kein Schulstoff! Die gekürzte Lösung für x1 lautet exakt

x1= -2 - 2/(5 - sqrt(17))^{1/3} - (5 - sqrt(17))^{1/3} mit sqrt(17)=Wurzel(17)

und kann beliebig genau berechnet werden.

Die letzten beiden komplexen Lösungen hattet Ihr bestimmt noch nicht.

Natürlich können die komplexen Nullstellen auch wieder per Polynomdivision berechnet werden:

einfach von Lösungsweg 1 nochmals teilen

(x³+6*x²+6*x+6) / (x+5.0466) ergibt quadratische Funktion, die per pq-Formel die beiden komplexen Ergebnisse liefert.

Lösungsweg 4 Bisektion

Iterationsrechner Beispiel 2 statt Beispiel 118

Nachteil: 

- man muss Suchbereich vorgeben, wo ein Nulldurchgang vorliegt.

- mehr Iterationen nötig als bei Newton