Sinus und Cosinus -- Periode, Nullstellen, Funktionswert

Question

Hallooo liebe Leute,

bräuchte mal eure Hilfe, habe leider gar keine Ahnung wie ich vorgehen soll... Erkennt man einige Antworten auf Anhieb ? Wäre euch sehr dankbar!

1. Periode

2. Erste Nullstelle

3. Zweite Nullstelle

4. Maximaler Funktionswert

5 Minimaler Funktionswert

Answer 1

Ja man erkennt einiges auf Anhieb, dazu muss man einfach nur wissen, wie der Sinus definiert ist. Kleines Beispiel:

A * sin (x), A ist die Amplitude, also die Höhe der des Verlaufes.

BSP 5*sin(x), geht dann von y = 5 bis y = -5

Weitere Beispiele:

Phase: sin(x + c), Sinus, der um c verschoben ist.

Bsp: sin(x +pi/2) Sinus der um pi/2 verschoben ist

---

Periode: Das bedeutet nichts anderes als die Wiederholung der Funktion, wann beginnt die Funktion wieder von vorne

---

sin(bx), b bewirkt eine Streckung oder Stauchung der Funktion, sodass die Lage der Nullstellen sich ändert.

---

sin(x) + c, Sinus der auf der y Achse verschoben wird

--

Grafik

hier einmal verschiedene Parameter und ihre Wirkung:

Anderes Beispiel:

Beachte bitte die Periode (rot eingezeichnet):

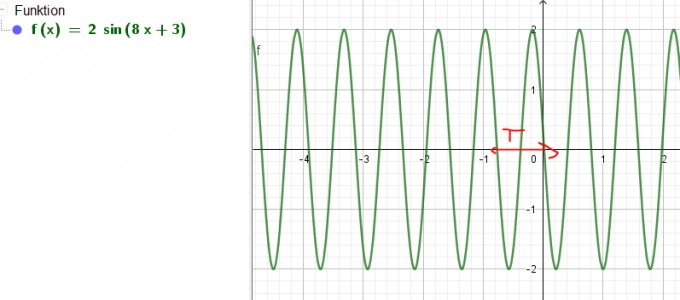
Mathematisch kann man das auch besser und präziser definieren, ich habe aber die Erfahrung gemacht, dass wenn man das etwas umgangssprachlich rüber bringt, auch mehr haften bleibt...

Comments

Die Periode kann man mehr oder weniger ablesen:

sin(bx+c)

Periode = T = 2*pi/b

---

Maximaler und Minimaler Funktionswert, siehe Amplitude (auch mehr oder weniger abzulesen)

---

Die Nullstellen ergeben sich aus der Periodenlänge (da auch im speziellen die Hälfte), der Ansatz ist f(x) = 0, ermittle daraus die erste Nullstelle. Die Zweite ergibt sich dann aus der Hälfte der Periode hinzuaddiert...

Formal:

x_2 (zweite NS) = x_1 (erste NS) + Hälfte der Periodenlänge

---

Also wäre jetzt in dem Fall die Periode (2*pi)/(8/5) ??? :/

Sorry, aber dieses Thema verstehe ich am aller wenigsten...

---

Ja genau! Das wäre richtig!

Vllt noch etwas genauer ausrechnen, also einfach in den Taschenrechner eingeben und fertig :)

---

Zur Kontrolle die Periode ist

(2*pi)/(8/5) = 5*pi/4

Nullstellen sind

1.) 0,

2.) 5*pi/8

3.) 5*pi/4

...

Fällt dir was auf?

---

Dass es mehrere Nullstellen gibt ? :/

Also die erste beginnend bei 0 und dann so weiter ?...

---

Hi die Nullstellen habe ich dir schon aufgeschrieben, es gibt unendlich viele, dir reichen aber die ersten beiden. unendlich viele, weil die Funktion ja kein Ende hat...

---

Das ist wirklich sehr sehr nett von dir :))) vielen lieben Dank.

---

Hier so sieht deine Funktion ungefähr aus die Nullstellen habe ich dir mal gekennzeichnet...

---

Klar kein Problem, ich hoffe du hast das etwas verstanden, das würde mich freuen!

---

Auf jeden Fall! :-)) Mir konnte es bisher leider niemand beibringen, aber jetzt sehe ich doch noch Hoffnung für mich. :-D

Das einzige, wo ich mir noch unsicher bin, ist minimaler und maximaler Funktionswert:-(

Kennst du vielleicht Seiten, wo es gute Übungsaufgaben + Lösungen gibt ?

---

Das mit dem minimalen Funktions Wert schaffst du auch, denke an das, was ich über die Amplitude gesagt habe.

hier noch eine Hilfestellung dazu, in meinem Eifer habe ich die Amplitude aber falsch eingezeichnet... 

---

Jetzt habe ich das auch verstanden :D Danke, vielen lieben Dank!!! Kann man dich als Nachhilfelehrer buchen ? :-D

---

Im ersten Bild ist die Amplitude richtig eingezeichnet... Das Maximum und Minimum kannst du aber an beiden Skizzen ablesen.

Answer 2

Periodenlänge
cos(0) bis cos(2π)

cos(0) = cos(8/5 * x+ 3/2)
0 = 8/5 * x+ 3/2
x = -15/16

cos(2π) = cos(8/5 * x+ 3/2)
2π = 8/5 * x+ 3/2
x = 5/4 * π - 15/16

( -15/16 - ( 5/4 * π - 15/16 )
- 5/4 * π
|  - 5/4 * π |
Periodenlänge = 5/4 * π = 3.927

rot Periodenlänge 3.927

Bei Bedarf weiter fragen.

Answer 3

a) Periode

b = 2·pi/T --> t = 2·pi/b = 2·pi/(8/5) = 5/4·pi = 3.927

b) Nullstellen

f(x) = 7/4·COS(8/5·x + 3/2) = 0

COS(8/5·x + 3/2) = 0

8/5·x + 3/2 = pi/2 ± k·pi

8/5·x = pi/2 - 3/2 ± k·pi

x = 5/8·(pi/2 - 3/2 ± k·pi) = 5/16·(pi - 3) ± 5/8·pi·k

x1 = 5/16·(pi - 3) = 0.0442

x2 = 5/16·(pi - 3) + 5/8·pi = 15·(pi - 1)/16 = 2.0077

c) Maximale und Minimale Funktionswerte

ymin = - 7/4 = - 1.75

ymax = 7/4 = 1.75