Hilfe beim Lösen des Integrals

Question

Ich brauche Hilfe beim lösen dieses Integrals mit dem angegebenen Grenzen. n soll hierbei 3 sein bzw. allgemein ungerade. Über Hilfe würde ich mich sehr freuen!

LG und

Answer 1

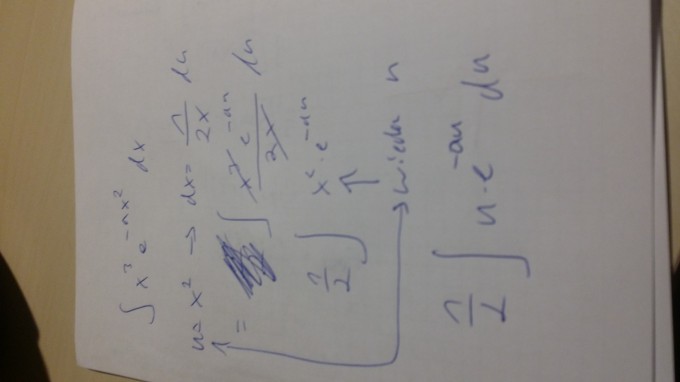
Hier gibt es mehrere Möglichkeiten, substituiere im Exponenten der E Funktion, oder und nutze die partielle Integration. Ist etwas Schreibarbeit aber führt zum Ziel.

Substitution ist x^2 = u, dann erhältst du

Integral von  1/2 *  ue^{-au}, du

zieh das 1/2 raus und integriere mit partieller Integration.

Comments

Ich hoffe, dass dich der Ansatz weiter bringt. Weil ich das Bild leider nicht drehen kann..

---

ja genau den Ansatz hatte ich auch aber mein Problem ist das ich nicht weiß wie ich das Integral über diese Grenzen bilden soll also von minus bis plus unendlich. Wenn ich normal nur die Stammfunktion bilden möchte ist das kein Problem. Ich dachte man müsste den Term so umformen, dass man das Gauss-Integral erhält, welches einen definierten Wert bildet:

---

Ja die Idee gefällt mir, aber es gibt da dann ja leider noch die konstante... Ich würde zunächst die Stammfunktion berechnen, wenn die Grenzen eingesetzt werden, wird sich da mit Sicherheit was raus kürzen

Answer 2

wenn n ungerade ist kann aufgrund der Symmetrie nur 0 herauskommen. Lediglich die Konvergenz muss noch bewiesen werden.

Rechenlastigere Ausführungen finden sich z.B hier:

http://matheplanet.com/default3.html?call=viewtopic.php?topic=142186&ref=https%3A%2F%2Fwww.google.de%2F