Analysis: Mengen von u.a. (A^c)^c

Question

Es seien A und B Teilmengen von einer Menge X. Berechnen Sie folgende Mengen:

1.) Wir setzen A^c := X\A. Berechnen Sie folgene Mengen: (A^c)^c.
Tipp: A= (A^c)^c. Beweisen Sie dies.

2.) A ∩ A^c

3.) A ∪ A^c

4.) ((A^c ∪ B) ∩ (A ∩ B^c))

Bei 1.) weiß ich gar nicht so richtig, wie ich anfangen soll. Außer eventuell Formeln umstellen...

Bei 2.) habe ich schon raus, dass eine leere Menge rauskommen müsste (ich hoffe das stimmt auch). Ich weiß bloß nicht, wie ich es mathematisch korrekt aufschreiben kann..

Bei 3.) habe ich schon mal (r ∈ A) ∧ ¬(r ∈ X) ∨ (r ∈ A)
Aber weiter komme ich nicht.

Mit 4.) komme ich gar nicht zurecht...

Ich hoffe, einer kann mir helfen, sodass ich es verstehe. 
Ich habe davon noch viele weitere Aufgaben, die ich lösen muss, aber das versuche ich auch erst einmal alleine...

Comments

Vielen Dank für die Antwort.

Ich hab es verstanden :)

LG

Answer 1

4.) ((A^c ∪ B) ∩ (A ∩ B^c))

Bei 1.) weiß ich gar nicht so richtig, wie ich anfangen soll. Außer eventuell Formeln umstellen...

Mengengleichheit  X=Y beweist man meistens so:

Sei x∈X ==>  ...  ==> ...   ==>  x∈ Y 

und dann umgekehrt 

Sei x∈y   ==>  ...  ==> ...   ==>  x∈ X

Hier wäre das also so:

Sei x ∈ (A^c)^c  ==> (nach Def. )     x ∈ X \  (A^c)   

==>  ( Def. von \ )             x ∈ X    ∧  x∉  (A^c)   

==>  ( Def. von ^c )             x ∈ X    ∧  x∉   X\A 

==>  ( Def. von  \  )             x ∈ X    ∧   nicht (     x ∈ X  ∧  x∉ A  ) 

==>  ( De Morgan  )             x ∈ X    ∧      ( x ∉ X     ∨   x∈ A  ) 

Da nun sowohl    x ∈ X  als auch x ∉ X     ∨   x∈ A

wahr sind, folgt  x∈ A ; denn der andere Teil der Oder-Aussage ist ja falsch.

Versuche ähnlich:    x∈ A ==>   (A^c)^c.      zu zeigen, dann hast du die Gleichheit.

Bei 2.) habe ich schon raus, dass eine leere Menge rauskommen müsste (ich hoffe das stimmt auch). Ich weiß bloß nicht, wie ich es mathematisch korrekt aufschreiben kann..

Nimm an es gibt     x∈ A   und    x∈ A^c    und führe dies zu einem Widerspruch,

dann gibt es kein gemeinsames Element von den beiden, also ist die Schnittmenge leer.

Bei 3.) habe ich schon mal (r ∈ A) ∧ ¬(r ∈ X) ∨ (r ∈ A) 

Genauer wohl so : Das Ergebnis ist     A ∪ A^c = X    .

Beweis mit deinem (korrigierten [Vereinigungsmenge ergibt "oder"

und mit der Negation ist was faul ]]

    Ansatz: Sei r ∈ A ∪ A^c 

==>  (r ∈ A) ∨     (r ∈ A^c )

==>  (r ∈ A) ∨     (r ∈ X\A)

==>  (r ∈ A) ∨    ((r ∈ X) ∧ (r ∉ A))

==>  ((r ∈ A) ∨ (r ∈ X))    ∧  ( ( r ∈ A) ∨ (r ∉ A))

Der zweite Teil ist immer wahr und weil A Teilmenge von X ist

besagt der erste Teil nur   r ∈ X.

Dann noch die andere Richtung zeigen

 r ∈ X. ==>  r ∈ A ∪ A^c 

it 4.) komme ich gar nicht zurecht...

4.) ((A^c ∪ B) ∩ (A ∩ B^c)) 

Kann man auch aufmalen um es sich vorzustellen (aus Versehen doppelt)

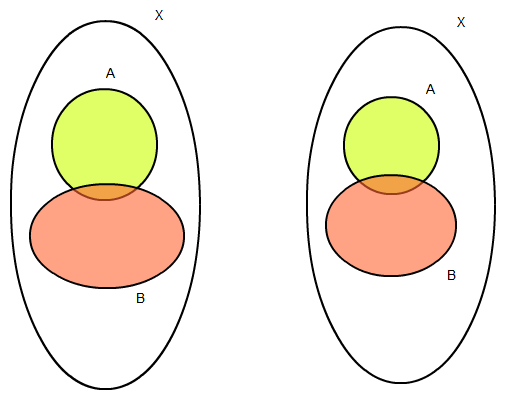
Dann ist (A^c ∪ B) alles was in A^c  (also außerhalb vom grünen) 

oder in B (also im braunen) liegt. Das heißt, das ist alles 

außerhalb vom grünen, es kommt nur noch die Schnittmenge 

von braun und grün dazu.

(A ∩ B^c)  Das ist alles außerhalb von B, was in A liegt

also sozusagen das grüne ohne die Schnittmenge von A und B.

Dann ist also   ((A^c ∪ B) ∩ (A ∩ B^c)) 

die Schnittmenge dieser beiden, das wäre dann wieder die leere Menge.