Binomischer Lehrsatz: Ungleichungen beweisen

Question

komme beim Beweis der folgenden zwei Ungleichungen nicht weiter:

Seien x und y positive reelle Zahlen und n eine natürliche Zahl echt größer als 1. Man soll den Binomischen Lehrsatz verwenden, um diese Ungleichungen zu beweisen:

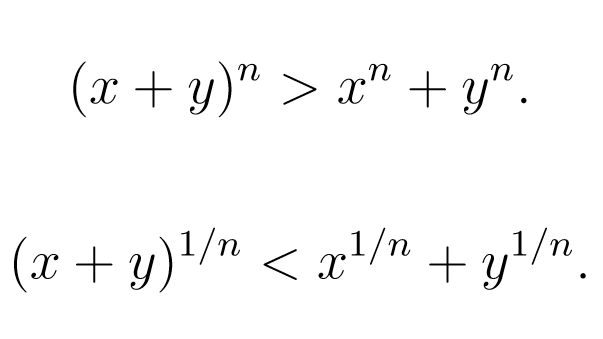
Bei der ersten Ungleichung habe ich $$ (x+y)^n $$ mit dem Binomischen Lehrsatz so aufgeschrieben: $$ \sum $$ (n über k) * x^{n-k} * y^k

Bei der zweiten dann analog: $$ \sum $$ x^{(n^-1)-k} * y^k

Ich weiß jedoch nicht, wie ich damit zeigen soll, dass die Ungleichungen gelten.

Gruß

Comments

a) ist klar:

(x+y)^n =x^n + irgendwas + y^n , wobei das irgendwas >0 ist, da x und y positiv sind. Das irgendwas kannst du dem binomischen Lehrsatz entnehmen.

---

Bei (b) vielleicht$$\left(x^\frac1n+y^\frac1n\right)^n=x+\underbrace{\sum_{k=1}^{n-1}\binom nkx^{\frac{n-k}n}y^\frac kn}_{>0}+y>x+y.$$Nun noch \(n\)-te Wurzel ziehen.