Lösungsmenge einer Ungleichung beweisen

Question

kurze Frage:

ax ≤ bx ≤ cx , L = [x₁,x₂]

Wenn ich eine Ungleichung habe und die Lösung als Intervall bekannt ist, wie beweise ich das es sich um die Lösung handelt?

Meine Idee wäre ja x₁ in den ersten Term und x₂ in den zweiten Term einzusetzen und in der Mitte x auszurechnen.

Dann müsste ich doch

x₁ ≤ x ≤ x₂

erhalten und damit wäre es doch bewiesen oder?

Answer 1

Stell einmal ein Foto der Aufgabe ein.

Ansonsten kann ich nur sagen

ax ≤ bx ≤ cx

Für x > 0 gilt
ax ≤ bx ≤ cx   | : x
a ≤ b ≤ c

Für x < 0 gilt
ax ≤ bx ≤ cx   | : x
a ≥ b ≥ c

Comments

Das wäre die Aufgabe.

Ich hab nochmal etwas recherchiert und die Ungleichung soll aufgespalten werden und damit könne man die Lösung berechnen.

Ich komme jedoch nicht auf diese Werte

---

Ich würde die Ungleichung in 2 Teile
aufspalten.
- linker und mittlerer Term
- mittlerer Term und rechter Term

und dann die Lösungen berechnen
und die Schnittmenge feststellen.

---

Mich stört dabei die Wurzel. Wenn ich eine Ungleichung davon nach x ausrechnen will bleibt bei mir immer eine Potenz übrig.

Könntest du mir eine Seite kurz vorrechnen?

---

Def Bereich 1 + x ≥ 0
x ≥ -1
Für die Ungleichung wurde zunächst der Spezialfall
der Gleichheit / Nullstellen berechnet.
Hier die kurze Berechnung.

( -1 | 0 )
( 0 | 0 )
( 3 | 0 )  | durch das quadrieren bedingt ist diese Lösung
eine Scheinlösung.

Bereiche die zu überprüfen sind
x < -1  ( außerhalb des Def-Bereichs )
-1 .. 0
0 .. ∞

Dann wurde nachgeschaut was herauskommt wenn ein
x-Wert zwischen den Nullstellen in die Ausgangsgleichung
eingesetzt wird.

links ( -0.5 ) = 0.625
rechte Seite ( -0.5 ) = 0.707
Für den Bereich -1 bis 0 stimmt die Ausgangsgleichung

links ( 1.5 ) = 0.625
rechte Seite ( 1.5 ) = 1.58
Für den Bereich 0 bis ∞ stimmt die Ausgangsgleichung
Lösungsmenge
-1 bis ∞

Alles unterhalb der x-Achse gehört zur
Lösungsmenge

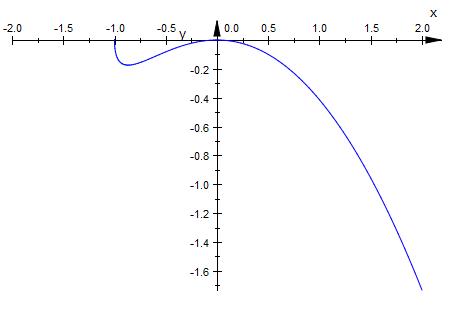
Und jetzt dasselbe mit dem anderen Teil der
Ausgangsgleichung.
Dann die Schnittmenge feststellen.

Ob´s einfacher geht weiß ich nicht.

---

Ich denke ich hab's verstanden

---

Ist nicht ganz so einfach.
Falls du noch Fragen hast dann
wieder melden.

---

Ich komme beim rechten aber nur auf x = 0, wo ist mein Fehler? 

---

Deine Lösung ist richtig.
x = 0 ist eine Nullstelle
Eingangsvoraussetzung
x ≥ -1 ( wegen der Wurzel )

Es müssen nun die Bereiche
-1 bis 0
und 0 bis ∞ geprüft werden
x = - 0.5
√ ( 1 - 0.5 ) ≤ 1 - 0.5/2
stimmt

Und der Bereich
x > 0
x = 0.5
√ ( 1 + 0.5 ) ≤ 1 + 0.5/2
stimmt auch
 
Der Ausdruck √ ( 1 + x ) ≤ 1 + x/2
stimmt für [ -1; ∞ [

Die Lösungmenge der Aufgabenstellung ist
[ -1; ∞ [

[ - 1; 1 ] ist in meiner Lösung auch enthalten
wäre aber eine Einschränkung.

Setze x = 3 einmal in die Ausgangsgleichungen
ein.

---

-2  ≤  2  ≤  2.5