Steckbriefaufgabe. Sattelpunkt im Koordinatenursprung

Question

Moinsen, 

Ich sitze momentan an einer Aufgabe und bräuchte Hilfe.

Die Aufgabenstellung lautet: Der Graph einer ganzrationalen Funktion dritten Grades geht durch den Koordinatenursprung und hat in S (-1/-1/3) einen Sattelpunkt. Wie lautet die Funktion?

Ein detaillierter Lösungweg wäre lukrativ.

Comments

Lukrativ erscheint mir in dem Zusammenhang ein merkwürdiger Begriff.

---

Inwiefern beantwortet das meine oben gestellte Frage? Garnicht, genau. Sinnvolle Antworten bevorzuge ich mehr.

---

Ja ich habe deine Frage ja auch nicht beantwortet, sondern kommentiert. Das ist nicht das gleiche. Du bist ganz schön patzig dafür dass du diejenige mit dem Anliegen bist.

---

Jeder hat so seine eigenen Herangehensweisen zu Interpretieren.In Ordnung, vielen Dank für den Hinweis!

---

Hast du die andere Aufgabe verstanden?

Answer 1

Hallo letra, 

f(x) = ax³ + bx² + cx + d      (allgemeine Form einer Funktion 3. Grades)

f geht durch Ursprung:

f(0)  = 0   →    d  = 0     →   f(x) = ax³ + bx² + cx 

f '(x)  =  3·a·x² + 2·b·x + c

f "(x)  = 6·a·x + 2·b

Sattelpunkt (-1 | -1/3):

Ein Sattelpunkt ist ein Wendepunkt mit waagrechter Tangente:

f(-1) = -1/3    ⇔    - a + b - c  =  - 1/3     (G1)

f "(-1) = 0      ⇔     2·b - 6·a = 0             (G2)

f '(-1) = 0       ⇔    3·a - 2·b + c = 0        (G3)

Wenn du G3 + G1 rechnest, fällt c weg  und du musst mit der neuen Gleichung und G2 ein LGS mit den 2 Unbekannten a und b lösen. Deren Werte kannst du dann in G1 einsetzen und c bestimmen.

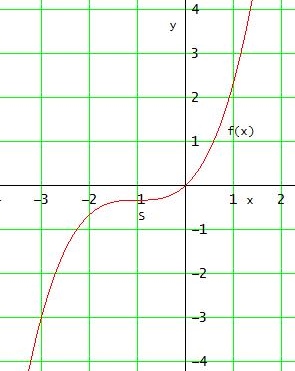
[ Kontrolllösung:  f(x)  =   1/3·x³ + x² + x ]   

Gruß Wolfgang. 

P.S.  "lukrativ" solltest du wirklich mal nachschlagen :-)

Answer 2

Der Graph einer ganzrationalen Funktion dritten Grades geht durch den Koordinatenursprung und hat in S (-1|-\( \frac{1}{3} \) ) einen Sattelpunkt. Wie lautet die Funktion?

Ich verschiebe den Graphen  um \( \frac{1}{3} \) nach oben S´(-1|0)  und P(0|\( \frac{1}{3} \))

f(x)=a*(x+1)^3

f(0)=a    a=\( \frac{1}{3} \)

f(x)=\( \frac{1}{3} \)*(x+1)^3

Nun \( \frac{1}{3} \) nach unten verschieben:

p(x)=\( \frac{1}{3} \)*(x+1)^3-\( \frac{1}{3} \)