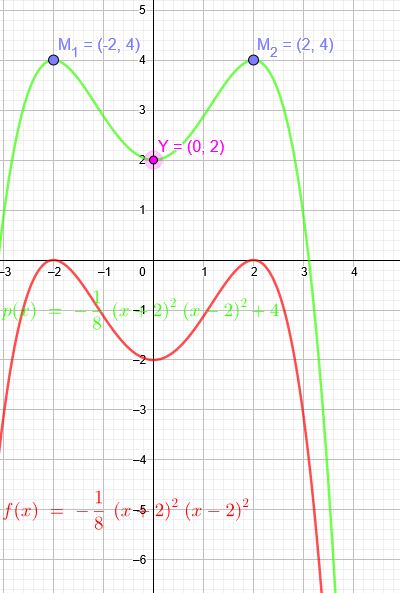
Bestimme die Gleichung einer ganzrationalen Funktion vierten Grades, deren Graph achsensymmetrisch zur y-Achse verläuft, diese bei 2 schneidet und in M \((2|4)\) ein Maximum hat.
\(M_1 (2|4)\) ein Maximum, somit auch bei \(M_2(-2|4)\)
\(M_2(-2|4)\) um 4 Einheiten nach unten verschieben : \(M_2(-2|0)\)
\(f(x)=a(x+2)^2(x-2)^2\)
\(Y(0|2)\)→\(Y´(0|-2)\):
\(f(0)=a(0+2)^2(0-2)^2=16a=-2\)
\(a=-\frac{1}{8}\)
\(f(x)=-\frac{1}{8}(x+2)^2(x-2)^2\)
um 4 Einheiten nach oben verschieben:
\(p(x)=-\frac{1}{8}(x+2)^2(x-2)^2+4\)