Hallo Andurs,
Allgemein kann man sagen, dass sich das Gewicht berechnet aus:
$$\int_V \delta(x,y,z) \space \text{d}V $$
aber das ist weder ein Dreifachintegral noch eine Rechenvorschrift. Ich denke hier bieten sich zwei Möglichkeiten an, dies aufzulösen. Einmal nur in kartesischen Koordinaten mit \(dV = \text{d}x \space \text{d}y \space \text{d}z\):
$$\int_0^h \int_{-a}^{+a} \int_{-\sqrt{a^2-y^2}}^{+\sqrt{a^2-y^2}}\delta(x,y,z) \space \text{d}x \space \text{d}y \space \text{d}z$$
oder unter zu Hilfenahme von Polarkoordinate mit \(x= r \cdot \cos \varphi, \space y= r \cdot \sin \varphi\). Wobei man sich hier Gedanken machen muss, wie das \(\text{d}V\) aussieht. Dazu eine kleine Skizze:
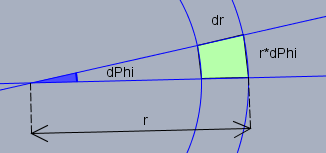
Ich habe aus dem Zylinder einen Ring mit der Breite von \(\text{d}r\) heraus geschnitten und daraus wiederum ein kleines Tortenstück mit dem Winkel \(\text{d}\varphi\) . Dann hat dieses Tortenstück (markierte Fläche) eine Grundfläche von \(r \cdot \text{d}\varphi \space \text{d}r\). Betrachte ich noch die Höhe \(\text{d}z\) des Stücks, so ergibt sich
$$\text{d}V= r \cdot \text{d}\varphi \space \text{d}r \space \text{d}z$$bzw.:
$$\int_0^h \int_{0}^{a} \int_{0}^{2\pi}\delta( r \cdot \cos \varphi,r \cdot \sin \varphi,z) \cdot r \space \text{d}\varphi \space \text{d}r \space \text{d}z$$
Welches von beiden Verfahren man wählt, hängt von der Funktion \(\delta(x,y,z)\) ab. Im Allgemeinen wird es mit den Polarkoordinaten einfacher sein. Mal angenommen, \(\delta\) sei konstant - etwa \(\delta(x,y,z)=\rho\). So erhält man:
$$\begin{aligned} G &= \int_0^h \int_{0}^{a} \int_{0}^{2\pi} \rho \cdot r \space \text{d}\varphi \space \text{d}r \space \text{d}z \\ &= \rho \int_0^h \int_{0}^{a} 2\pi r \space \text{d}r \space \text{d}z\\ &=\rho \pi \int_0^h a^2 \space \text{d}z \\ &= \rho \pi a^2 h \end{aligned}$$
Gruß Werner
PS.: ich habe hier noch einen netten Link dazu gefunden: https://www.tu-chemnitz.de/physik/OSMP/cvb_ph1/ph1_tut_sk_01.pdf.