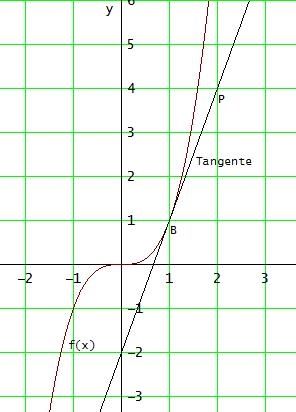
f(x) = x3 , f '(x) = 3x2 x ∈ [0 , 2 ] ; P(2|4)
Die Gerade durch den Punkt P( xp | yp ) mit der Steigung m hat die Gleichung
y = m • ( x - xp ) + yp [ Punkt-Steigungs-Formel ]
Die Steigung der Tangente im Berührpunkt B( xB | yB ) = (xB | xB3) ist gleich f '(xB) = 3xB2
Tangente: y = f '(xB) · (x - 2) + 4 #
Berührpunkt einsetzen (ergibt Bestimmungsgleichung für xB ) :
xB3 = 3xB2 · ( xB - 2 ) + 4 = 3xB3 - 6xB2 + 4
2xB3 - 6xB2 + 4 = 0 ⇔ xB3 - 3xB2 + 2 = 0 → xB = 1
Polynomdivision (x3 - 3x2+2):(x-1) und pq-Formel ergeben noch x2,3 = 1 ±√3 ∉ [ 0 , 2 ]
xB = 1 in # einsetzen:
Tangente: y = 3 · (x - 2) + 4 → y = 3x - 2
Gruß Wolfgang