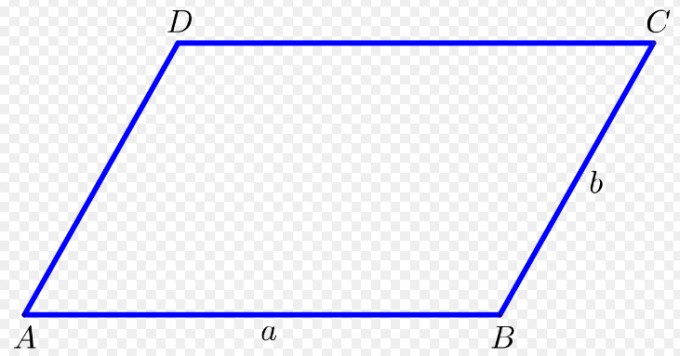
gehen wir davon aus dass die Punkt A,B,C,D gegeben sind. Frage: Stelle die Bedingungen auf,dass ein Viereck ABCD ein Parallelogramm,aber kein Rechteck ist.
Bedingung(das dass Viereck eine Parallelogramm ist): Vektor AB = Vektor DC , Zwischenfrage: würde hier auch die Bedingung: Vektor AD = Vektor BC funktionieren, dass es ein Parallelogramm ist?
Bedingung(das dass Parallelogramm kein Rechteck ist): Skalarprodukt von Vektor AB und Vektor AD ≠ 0