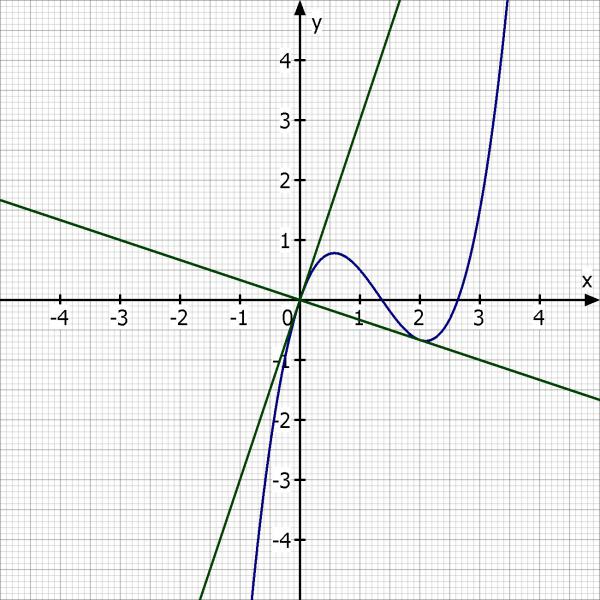
f(x) = 5/6·x^3 - 10/3·x^2 + 3·x
f'(x) = 5·x^2/2 - 20·x/3 + 3
Tangente vom Ursprung an den Graphen
(f(x) - 0) / (x - 0) = f'(x)
(5/6·x^3 - 10/3·x^2 + 3·x) / x = 5·x^2/2 - 20·x/3 + 3
5·x^2/6 - 10·x/3 + 3 = 5·x^2/2 - 20·x/3 + 3
5·x^2 - 20·x + 18 = 15·x^2 - 40·x + 18
10·x^2 - 20·x = 0
x·(10·x - 20) = 0
x1 = 0
x2 = 2
f(0) = 0
f'(0) = 3
t1(x) = 3 * (x - 0) + 0 = 3x
f(2) = - 2/3
f'(2) = - 1/3
t2(x) = -1/3 * (x - 2) - 2/3 = - x/3
Skizze: