Basis eines Kerns (lineare abbildungen)

Question

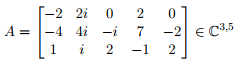
Hallo :) Gegeben ist dieses A. Die Aufgabe ist es, den Kern(A) zu bestimmen. Ich habe nun unsere Matrix in Zeilenstufenform gebracht, gleich 0 gesetzt und dann rückwärts eingesetzt und bin nun auf das Ergebnis gekommen, dass der Kern(A)=

[3ix4-2ix5-x5+x4]

[3x4-2x5+ix5      ]

[-3ix4+2ix5         ] E  C^3 ist.   Wie komme ich nun auf die Basis vom Kern(A)

Unser Rang ist 3 und unsere Dimension 2.

Answer 1

Deine Elemente sind linear unabhängig und spannen den Kern auf, also ist es automatisch eine Basis.

Comments

Also ist eine Basis z.b.

(1 für frei wählbare variablen im Kern eingesetzt)=[i , 1+i , -1i] und [0,0,0] ?

---

Möchtest du wirklich die Basis des Kerns bestimmen?
Was hast du denn für den Kern raus?

---

Ich habe oben mein Kern schon angegeben. Ist der falsch?

Ja die Aufgabe lautet, Basis von Kern(A)

---

Elemente im Kern müssten doch 5x1-Vektoren sein.

---

ahh okay, also muss ich unter mein x1,x2,x3 noch x4 und x5 schreiben

---

Genau.

Du erhältst bei dir nun, dass zwei Variablen frei wählbar sind.
Setze einmal x4 = 0 und x5=1  und einmal x4=1 und x5=0 und du erhältst zwei unabhängige Vektoren, die deinen Kern aufspannen, also eine Basis des Kerns.