Die nebenstehende Abbildung zeigt einen Würfel mit der Seitenflächendiagonalen d1 und der Raumdiagonalen d2.

Question

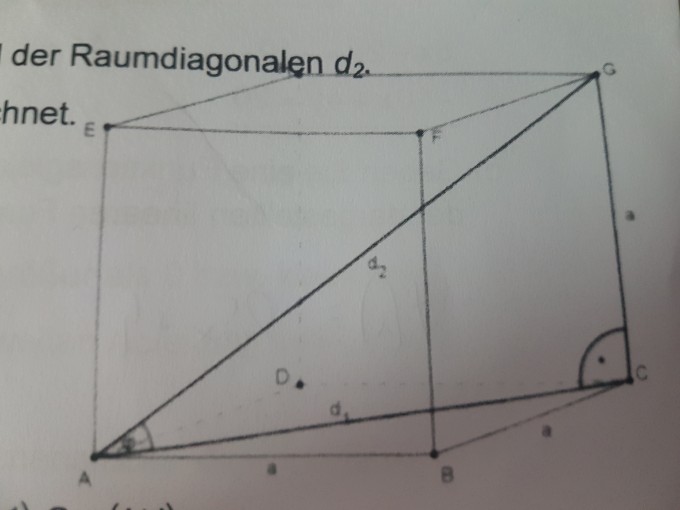
Begründen Sie, warum d1 = a*√2 und d2 = a*√3 gilt.

Ich habe leider keine Erklärung gefunden. Nur, das d1 = a*√2 die Flächendiagonale ist und d2 = a*√3 die Raumdiagonale 

Berechnen Sie α.

Ich habe zwei Rechenwege im Internet gefunden. Da gäbe es arctan(1/√2) und arctan(√2). Rechtwinkliges Dreieck, daher müssen α und β einen Winkel von 90° einschließen. Mit arctan(1/√2) kommt 35.264° heraus, mit arctan(√2) 54,74°.
Auf der Zeichnung sehe ich ja, dass α kleiner als β ist, somit muss α=35.264° haben. Was wäre aber, wenn die Zeichnung gar nicht gegeben wäre?

Answer 1

Alles über den Pythagoras

Flächendiagonale
d1^2 = a^2 + a^2 = 2*a^2
d1 = √ ( 2a^2 ) = a * √ 2

Raumdiagonale
d2^2  = Flächendiagonale ^2 + a^2
d2^2  = 2 * a^2  + a^2 = 3 * a^2
d2 = √ ( 3a^2 ) = √ 3 * a

Comments

Guten Morgen und Danke, Georg. 
Gut, das wäre dann die Begründung für d1 und d2. Ich verstehe aber leider nicht den Zusammenhang zu α in diesem Fall. Ist es so, dass α den kleineren Winkel hat, weil α sowohl die Flächen- als auch die Raumdiagonale einschließt?

---

Ich hatte die Frage
Berechnen Sie α.
nicht gesehen.

Winkel im Dreieck unten
45 ° - 90 ° - 45 °

Räumliches Dreieck ( rechtwinklig )
Grundseite a * √ 2
Höhe a
tan ( α ) = a /  ( a * √ 2 ) = 1 / √ 2
tan ( α ) = 0.707
α  =  35.26 °

Answer 2

Die Erklärung liefert in beiden Fällen Pythagoras. In einem Quadrat mit der Seitenlänge a und der Diagonalen d gilt a²+a²=d²und deshalb d= √(2a²)= a√2. Die Raumdiagonale r ist die Hypotenuse eines rechtwinkligen Dreiecks mit den Katheten d und a,also d²+a²=r². Hier d² =2a² einsetzen.

Comments

Danke dir, Roland. Rein interessehalber - Unser Prof. hat uns erzählt, dass es bei mehrdimensionalen Würfeln auch d3=√4*a (wenn ich mich recht erinnere). Wie würde die dann heißen?

---

Die Diagonale eines n-dimensionalen Würfels (was auchimmer das sein mag) ist d_n=a·√n. Ein zweidimensionalwr Würfel ist dann ein Quadrat und ein eindimensionaler Würfel ist eine Strecke. Die nächsthöhere Dimension entsteht durch Verschiebung der Vorgängerdimension entlang eines Vektors (hier der Länge a).

---

Sehr gut erklärt. Danke dir, Roland.