Zeigen Sie, dass 0,9 (periode) := 0,9999999... = 1 und welche Zahl die Dualzahl definiert.

Question

Eine unendliche Dezimalzahl x = 0,a₁a₂a₃a₄ . . . mit den Ziffern a_k ∈ {0; 1; 2;. . ., 9}, k ∈ ℕ, ist defi niert durch

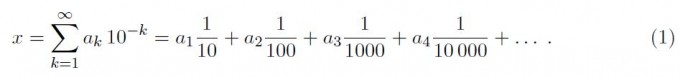
Eine Dualzahl erhält man, wenn a_k ∈ {0,1}, k ∈ ℕ, und in der Darstellung (1) die 10^-kdurch 2^-k ersetzt wird.

a) Zeigen Sie, dass 0,9 (periode) := 0,9999999... = 1 ist.

b) Welche rationale Zahl r = p/q, p,q ∈ ℕ, definiert die Dualzahl  0,01 (periode) = 0,010101010101...?

Answer 1

a) Sei ε > 0. Finde ein n, so dass 1 - ∑_k=1..n 9/10^k < ε ist.

Tipp: Wegen 1/10^m → 0 für m → ∞ gibt es ein p, so dass 1/10^p < ε. Es reicht also, zu zeigen, dass für jedes p ein n gibt, so dass 1 - ∑_k=1..n 9/10^k < 1/10^p ist.

b)

        0,0̅1̅
    = ∑_k=1..∞ 1/2^2k        (laut Definition)
    = ∑_k=1..∞ 1/4^k          (wegen Potenzgesetzen)
    = -1 + ∑_k=0..∞ 1/4^k  (wegen 1/4⁰ = 1, N.B. die Reihe fängt jetzt bei 0 an)
    = -1 + 1/(1 - 1/4)     (Grenzwert Geometrische Reihe)
    = 1/3

Answer 2

b) probier mal 10/99

(0.01 Periode

=1/10 ∑ (n=0 bis ∞) (1/100)^n )