Hi
$$\begin{pmatrix}1 & 10\\ 1 & 11.9\\ 1 & 13.1\\ 1 & 15.5\end{pmatrix}\cdot\begin{pmatrix}a_0\\ a_1\end{pmatrix} = \begin{pmatrix}17.57\\ 18.85\\ 20.2\\ 21.75 \end{pmatrix} \\A = \begin{pmatrix}1 & 10\\ 1 & 11.9\\ 1 & 13.1\\ 1 & 15.5\end{pmatrix}, \quad b = \begin{pmatrix}17.57\\ 18.85\\ 20.2\\ 21.75 \end{pmatrix} \\A^T\cdot A\cdot \begin{pmatrix}a_0\\ a_1\end{pmatrix} = A^T\cdot b \\\begin{pmatrix}4 & 50.5\\ 50.5 & 653.47\end{pmatrix}\cdot \begin{pmatrix}a_0\\ a_1\end{pmatrix} = \begin{pmatrix}78.37\\ 1001.76\end{pmatrix}\\$$
LGS lösen \(\Rightarrow \)
$$ a_0 \approx 9.79984, \ a_1 \approx 0.775656 \\z = 9.79984 + 0.775656 \ x $$
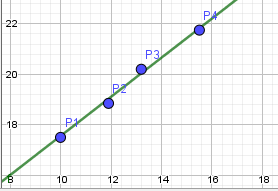
Grüße