:)
Zu folgender Aufgabe hätte ich eine Frage:
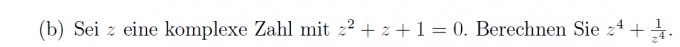
Ich weiß nun, dass die komplexe Zahl so beschrieben wird: z= a+bi. Allerdings komme ich echt nicht mehr weiter, v.a. weil wir so eine Aufgabe nicht durchgenommen haben. Wäre über eine Hilfestellung/ Lösungsvorschlag sehr dankbar!