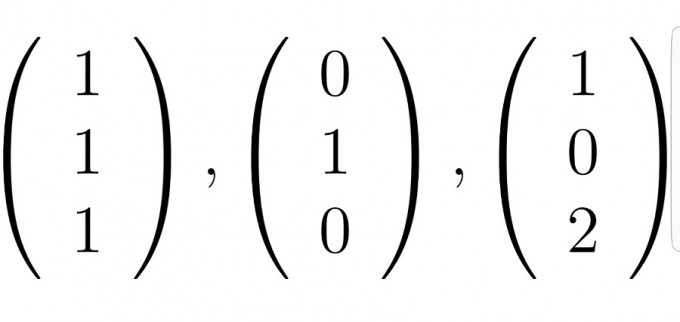Abbildungsmatrix bestimmen mit Vektoren

Question

Hallo zu zeigen ist, dass es eine eindeutig bestimmte R-lineare Abbildung $$ R^3 -> R^3 $$ gibt, welche die unten stehenden Vektoren auf die obenstehenden abbildet.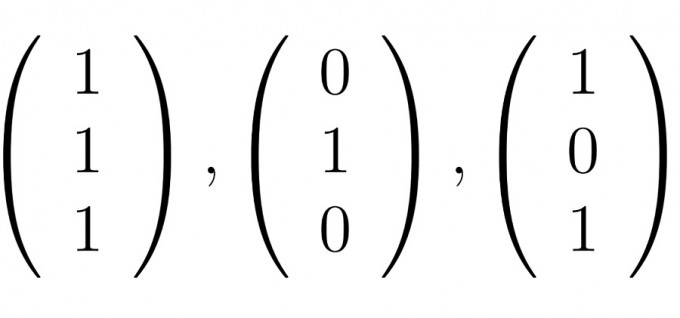

Die Abbildungsmatrix von f in der Standardbasis R^3 soll auch bestimmt werden. Für die Abbildungsmatrix braucht man doch eine Zuordnungsvorschrift. Wie erhält man die? Die Vektoren sind ja fast identisch, aber sehe nicht, wie man die Matrix ohne Vorschrift bekommt.

Comments

Deine Vektoren passen nicht zum Aufgabentext. Fuer die angegebenen gibt es keine lineare Abbildung wie gewuenscht.

In jedem Fall wird es etwas damit zu tun haben, dass die Abbildung linear sein soll und nicht beliebig. Du kennst ja vielleicht diese Steckbriefaufgaben. So etwas aehnliches sollst Du hier auch machen: Die Abbildungsvorschrift rekonstruieren.

---

Stimmt, das zweite sollte auf das erste abgebildet werden, also umgekehrt. Danke für den Hinweis, werde es so versuchen.

Answer 1

Es gibt KEINE solche Abbildung; denn gäbe es eine,

dann müsste

f(1;1;1)

= f(0;1;0) + f(1;0;1) sein, also einer der

drei unten angegebenen die Summe der anderen beiden.

Dem ist aber nicht so.

Comments

Die Vektoren unten sollen auf die Vektoren im oberen Teil des Beitrags abgebildet werden, sprich der umgekehrte Fall. Habe es versehentlich falsch rum gepostet. Wäre nett, wenn es jemand korrigieren würde.