Die Dreifachspiegelung sd •sb •sa ist eine Achsenspiegelung …

Question

ich hatte diese eine Teilaufgabe gerade in der Vorlesung und konnte sie nicht lösen. Kann mir jemand weiterhelfen?

Die Erste Aufgabe habe ich schon, die Frage ist an die 2. gerichtet.

Es  sei ein rechtwinkliges Trapez ABCD mit rechtem Winkel bei A und B gegeben . Wir definieren außerdem a, b, c, d, e und f wie in der  Zeichnung demonstriert.

1.Ersetzte die Dreifachspiegelung   sd •sb •sa durch eine Kongruenzabbildung.

2.Die Dreifachspiegelung sd •sb •sa ist eine Achsenspiegelung. Ermitteln Sie die Achse durch Spiegelungsrechnen und konstruiere  die Achse sowie das Bild von ABCD bei Spiegelung an der Achse mit einer Visualisierung ihrer Wahl wie z.B Geogebra.

Comments

Das ist die Zeichnung dazu.

---

Hallo Pia,

vor der Antwort könntest Du uns mal verraten, wie Ihr 'Spiegelrechnungen' grundsätzlich durchführt - allein von der Syntax her. Hier wäre es (für mich!) einfacher mit Abbildungen (sprich Matrizen) zu arbeiten. Habe aber erst heute Abend für eine ausführliche Antwort Zeit.

---

Werner- Salomon, ich hätte eine neue Frage die zu einem ähnlichen Thema ist. Könntest du mir das eventuell erläutern wenn du Zeit dazu irgendwann mal findest :-) Wäre sehr nett .

Answer 1

Hallo Pia,

Du hast leider auf meine Frage hinsichtlich der verwendeten Syntax des Spiegelrechnens nicht geantwortet. Ich mache es mir daher leicht und schreibe einfach, dass zwei Achsenspiegelungen an zwei parallelen Achsen einer Verschiebung \(v\) um den doppelten Abstand der Achsen gleichkommt. Das bedeutet:

$$s_d \circ s_b = v_{2\vec{AB}} \quad \quad d \parallel b \space \cap \space d \perp \vec{AB}$$

und eine Verschiebung um \(2\vec{AB}\) plus anschließende Spiegelung an einer parallelen Geraden \(a\) ist eine Gleitspiegelung \(g\)

$$s_d \circ s_b \circ s_a = v_{2\vec{AB}} \circ s_a = g_{a,|2\vec{AB}|} \quad \quad a \parallel \vec{AB}$$

und das ganze als Zeichnung

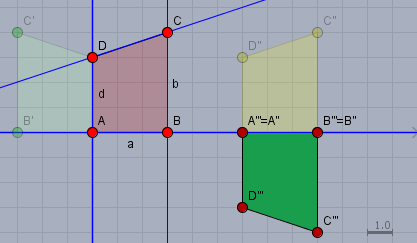
Das grünen Viereck ist das Bild von \(ABCD\) nach der Dreifachspiegelung.

Gruß Werner

Comments

Ist genau richtig. Entschuldige aber war gestern nicht mehr online. Wir haben die Aufgabe schon grob besprochen und hatten das selbe Ergebnis raus, aber deine Erläuterung ist um Längen besser.