1/4 X^3 -3X +4 in Linearfaktoren zerlegen

Question

1/4 X^3 -3X +4  weiß jemand wie man die aufgabe löst ?

1/4 x^3 -3x +4

kann mir jemand den Lösungsweg nennen ?

Nachtrag:

da steht: berechnen Sie für die durch ihre Funktionsgleichungen gegebene Funktionen die Nullstellen mit ihren Vielfachheiten.

Zerlegen Sie die Funktion in Linearfaktoren

Comments

Was genau ist zu lösen? Sollst du eine Funktion zeichnen? Eine Gleichung lösen? Da bräuchte man aber ein Gleichheitszeichen.

---

da steht: berechnen sie für die durch ihre Funktionsgleichungen gegebene Funktionen die Nullstellen mit ihren Vielfachheiten.

Zerlegen Sie die Funktion in Linearfaktoren

Answer 1

Hi,

zu lösen gibt es da nicht viel^^. Oder suchst Du die Nullstellen?

1/4x^3-3x+4 = 0   |*4

x^3-12x+16 = 0  

Nullstelle raten um Polynomdivision machen zu können. x=-4 ist Nullstelle

(x^3-12x+16):(x+4) = x^2-4x+4

 

Man erkennt die binomische Formel: x^2-4x+4 = (x-2)^2

 

Die Nullstellen sind also:

x₁ = -4   -> Vielfachheit 1

x_2,3 = 2   -> Vielfachheit 2

 

Grüße

Comments

da steht: berechnen sie für die durch ihre Funktionsgleichungen gegebene Funktionen die Nullstellen mit ihren Vielfachheiten.

Zerlegen Sie die Funktion in Linearfaktoren

 

Das hab ich ja schon alles gemacht. Noch sauber die Linearfaktorisierung aufgeschrieben:

y=1/4*(x-2)^2·(x+4)

Answer 2

Zu erst würde ich mir die Funktion mal anschauen. Das kannst du entweder per Hand, alles aufzeichnen oder vielleicht hast du ja auch einen Taschenrechner, der das kann. Ansonsten kannst du die Formel auch bei wolframalpha.com eintippen und dir die Funktion wiedergeben lassen. Wenn du allerdings in der Mathearbeit sitzt, dann musst du das ganze wohl durch ausprobieren herausfinden.

Das ganze ist nämlich wichtig, damit du dir die Nullstellen anschauen kannst. Wenn du das gemacht hast, dann arbeite mit dem Horner-Schema.

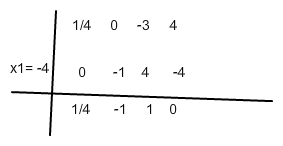
(Die erste stelle hast du bei -4 )

Das kannst du jetzt als quadratische Funktion aufschreiben

1/4 *x²  -1x  +1 = 0

Mit der PQ-Formel kannst du jetzt die letzten beiden Nullstellen rausfinden

 x²+px +q  -> -P/2 + - √(p/2)² -q

um auf diese Gleichung zu kommen, musst du die Zahl vor dem x² teilen

-> x² -4x +4

x₂ = 2 + √4-4 = 2

x₃ = 2 - √4-4 = 2

Hier siehst du, dass x2 und x3 eine doppelte Nullstelle ist. D.h. dass es einen Sattelpunkt auf der X-Achse Gibt

Die Linearfaktorzerlegung machst du mit dieser Formel

y = a*(x -x₁) * ( x -x₂) * (x - x₃)

-> y = 1/4 * (x +4) * (x -2) * (x - 2) = (x + 4) * (x - 2)²

 

Auch wenn die Antwort ein bisschen spät kommt, hoffe ich, dass ich hier jemanden helfen konnte. :) Falls noch Fragen da sind, dann immer her damit ;)