Zeigen, dass Untergruppenkriterium für kommutativen Ring und eine bestimmte Menge erfüllt ist.

Question

Für einen kommutativen Ring R sei

 

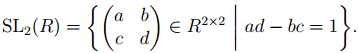
Weiter seien ℤ/5ℤ der Körper mit 5 Elementen und π: SL₂(ℤ) → SL₂(ℤ/5ℤ) durch

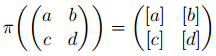
definiert.

Zeigen Sie, dass für jeden kommutativen Ring R die Menge SL₂(R) eine Untergruppe von GL₂(R) ist.

bestimmt zeigt man das "einfach" mit dem Untergruppenkriterium oder? Leider will mir das mit all den Matrizen nicht gelingen. Kann mir jemand zeigen wie man diese Aufgabe löst? , lg Laura (:

Answer 1

Hallo,

du musst zwei allgemeine Matrizen \( S \) und \( S' \) aus \( \textrm{SL}_2(R) \) multiplizieren und berechnen, ob für die resultierende Matrix die Gleichung \( ad - bc = 1 \) erfüllt ist:

\( S S' = \left(\begin{array}{rr}a & b \\ c & d\end{array}\right) \left(\begin{array}{rr}a' & b' \\ c' & d'\end{array}\right) = \left(\begin{array}{rr}aa' + bc' & ab' + bd' \\ ca' + dc' & cb' + dd' \end{array}\right) \),

\( (aa' + bc')(cb' + dd') - (ca' + dc')(ab' + bd') \)
\( = \dots = (ad - bc)(a'd' - b'c') = 1 \).

Ist \( S \in \textrm{SL}_2(R) \), so ist

\( S^{-1} = \frac{1}{ad - bc} \left(\begin{array}{rr}d & -b \\ -c & a\end{array}\right) = \left(\begin{array}{rr}d & -b \\ -c & a\end{array}\right) \)

die inverse Matrix, wie man gegebenenfalls nachprüft. Man erkennt leicht, dass \( S^{-1} \in \textrm{SL}_2(R) \) ist.

Grüße

Mister