Hallo Laura,
um eine Matrix als Produkt darzustellen, versuchst du am besten diese mittels bekannter Verfahren in Treppenform zu bringen. Da SL2 (R) ≤ GL2 (R) für jeden Ring R ist (das hast du ja schon gezeigt), gilt: Die Treppenform von A ist die Einheitsmatrix I2 . Achtung!: Du darfst nur die dir zur Verfügung gestellten Matrizen als Operanden benutzen (also beliebig multiplizieren geht nicht). Dein Produkt erhältst du wenn du die Inversen der benutzten Operanden in umgekehrter Reihenfolge ausführst.
Eine mögliche Lösung wäre damit:
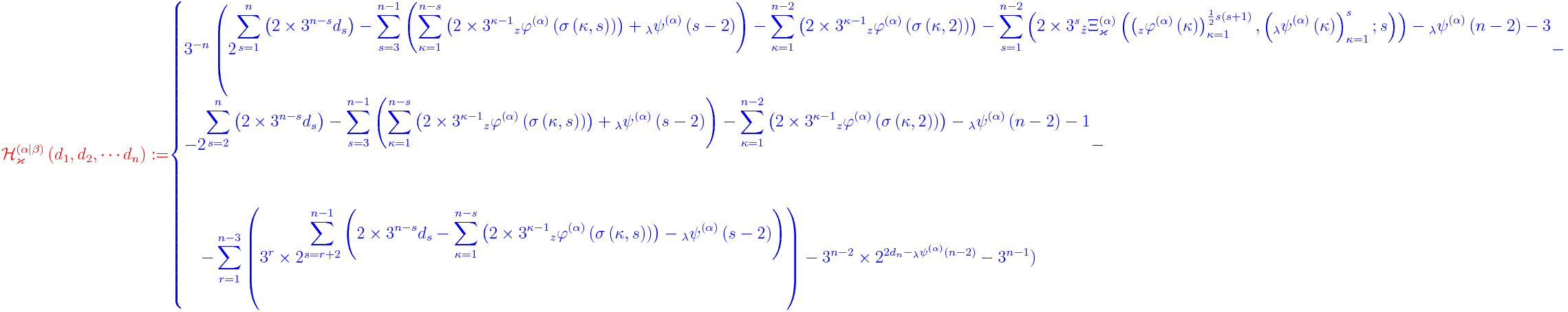
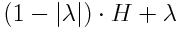
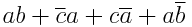
(A1 und A2 sind die beiden erlaubten Additionsmatrizen)
Versuch nachzuvollziehen warum die einzelnen Schritte funktionieren und rechne es selber nach. Warum gilt, dass A in Treppenform I2 ist? Warum darf man durch a teilen (bzw. warum muss a eine Einheit sein)?
Ich hoffe ich konnte dir weiter helfen.
Lg Jannis