Definitionsbereich von f(x,y) = [ ((x^2)+y)^{0,5} -x ]^{0,5} sowie Skizze vom Definitionsbereich

Question

Funktion:

\( f(x, y)=\sqrt{\sqrt{\left(\left(x^{2}\right)+y\right)}-x} \)

Ich suche Folgendes:

- Definitionsbereich von f

- Skizze von Definitionsbereich

- Wie verändert sich der Wert der Funktion näherungsweise , wenn ausgehend v P (0,1) eine Einheit in Richtung (2,1) geht ?

- Skizze der Isoquante mit c=1

Ich habe bei der Fallunterscheidung irgendwie schon Schwierigkeiten

ich hab diese 2 hier einmal vorerst x² + y ≥ 0 wird umgeformt zu y ≥ -x² und dann noch \( \sqrt{x^2 + y} \gt x \).

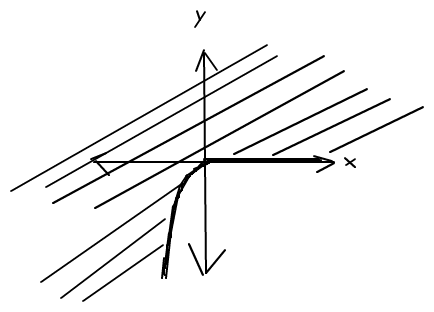
Laut Prof. sollte die Skizze so aussehen:

Answer 1

Erste Rechnung ist ja richtig:

y ≥ -x^2

Für x ≥ 0

√(x^2 + y) ≥ x
x^2 + y ≥ x^2
y ≥ 0

Für x ≤ 0

√(x^2 + y) ≥ x ist immer erfüllt. Damit ist nur die Bedingung für y bindent.


Damit ist der Definitionsbereich für
x ≥ 0, y ≥ 0
x ≤ 0, y ≥ -x^2

Skizziert ist das ja eigentlich schon recht gut.

Comments

- Wie verändert sich der Wert der Funktion näherungsweise , wenn ausgehend v P (0,1) eine Einheit in Richtung (2,1) geht ? 

f(0, 1) = 1
f(2, 2) = √(√6 - 2) = 0.6704399621

(√(√6 - 2) - 1) / (2^2 + 1^2) = √(√6 - 2)/5 - 1/5 = -0.06591200757

Ich hoffe das ist damit gemeint. Bin mir aber nicht sicher.

---

- Skizze der Isoquante mit c=1

√(√(x^2 + y) - x) = 1
√(x^2 + y) - x = 1
√(x^2 + y) = x + 1 für x > -1
x^2 + y = (x + 1)^2 
x^2 + y = x^2 + 2x + 1
y = 2x + 1

Skizze mit allen Angaben:

---

hey mathecoach , danke für deine Hilfe vorab !

ich hab eigentlich alles mitbekommen , außer das mit "bident" , das war mir neu .

ich hab bei der isoquante auch das gleiche , aber bei punkt c steht irgendwie etwas von

f nach x ableiten und
f nach y ableiten

und das sollte dann mit dem gradient irgendwie lösbar sein ... und hier komme ich grad wieder nicht weiter . wäre toll wenn du ( Sie ) mir noch helfen kannst ( könnten ) .

Vielen Dank nochmal ! lg !

---

Also die erste Ableitung nach x ist:

\( \frac{1}{2} · \left[\left(x^{2}+y\right)^{1 / 2}-x\right]^{(-0,5)} · 0,5 · \left(x^{2}+y\right)^{-0,5}-1 · 2 x \)

Ableitung nach y ist \( (0,5) · \left[\left(x^{2}+y\right)^{0,5}-x\right]^{0,5} · 0,5 · \left(x^{2}-y\right)^{-0,5} \)

Ich komme zum Ergebnis "-0,33".

Ja, stimmt!