Gebrochenrationale Funktionen (Nullstellen ; Polstellen; Grenzwerte; Asymptote)

Question

Komme bei dieser Aufgabe nicht weiter:

f(x)= (x^3+2x^2+x)/(x^4-13x^2+36)

Zerlegen Sie jeweils den Zähler und den Nenner der Funktionen in Linearfaktoren und
bestimmen Sie dann
- den Definitionsbereich
- alle Nullstellen
- alle Polstellen mit / ohne Vorzeichenwechsel
- alle hebbaren Unstetigkeiten einschließlich der Grenzwerte an diesen Stellen
- die Grenzwerte für x gegen unendlich und gegen minus unendlich
- die Asymptoten für x gegen unendlich.

Wäre sehr sehr sehr nett, wenn auch etwas dabie erklärt wird, will dieses Thema endlich ich meinen quadratschädel bekommen! ;-)

Answer 1

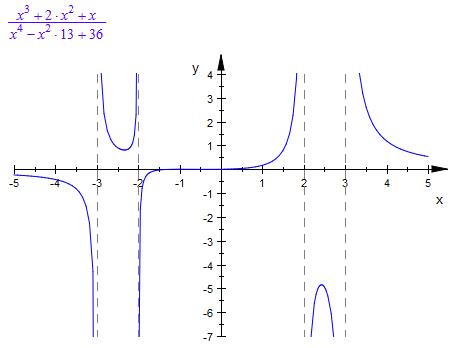
f(x)= (x3+2x2+x)/(x4-13x2+36)

zähler = (x^3+2*x^2+x)

x^3+2*x^2+x= 0
x * ( x^2 + 2 * x + 1 ) = 0
x * ( x + 1 )^2 = 0
Satz vom Nullprodukt
x = 0
und
x = -1
Zähler = x * ( x + 1 ) ^2

Nenner = x^4-13*x^2+36

x^4-13*x^2+36 = 0
ersetzen z = x^2
z^2 - 13 * z + 36 = 0

z = 4
und z = 9

x^2 = 4
x = ± 2
und
x^2 = 9
x = ± 3
Nenner = ( x - 2 ) * ( x + 2 ) * ( x  -3 ) * ( x +3 )

x * ( x + 1 ) * ( x + 1 )
--------------------------------------------

( x - 2 ) * ( x + 2 ) * ( x  -3 ) * ( x +3 )

D = ℝ \ { -2 ; + 2 ; - 3 ; 3 }
( Division durch 0 vermeiden )
Dies sind die Polstellen,

Genug fürs erste.

Comments

Bin dir echt was schuldig danke !!!

---

Eine Polstelle ist  vorhanden falls der
Nenner 0 ist. Ist der Zähler an der Stelle auch 0
dann ist es eine hebbare Lücke.
Ein Linearfaktor kommt dann sowohl im
Zähler wie im Nenner vor und kann gekürzt
werden.
Dies ist nicht der Fall.

Bestimmen sie dann
- alle hebbaren Unstetigkeiten einschließlich der Grenzwerte an diesen Stellen
Es gibt keine solche Stelle.

- Nullstellen
Eine Nullstelle liegt vor falls der Zähler eines
Bruches null ist.
0 durch irgendwas ist null
Zähler = x * ( x + 1 ) * ( x + 1 )
Ein Produkt ist dann null falls einer
der Faktoren null ist:
x = 0
und
x = -1

Kann noch weiter gehen bis alle
Teilfragen geklärt sind.

<!-- StartFragment -->

Bin dir echt was schuldig danke !!!

Als Dank beherzigst du bist Mitternacht :

Ich will Vater und Mutter ehren als ob Sie meine
Eltern wären .