Ich habe Probleme bei folgender Aufgabe:
Mein Ansatz: Ich muss zeigen dass das Integral von 0 bis Unendlich über g(x,y) =1 ist, jedoch komme ich leide nie auf eine 1.
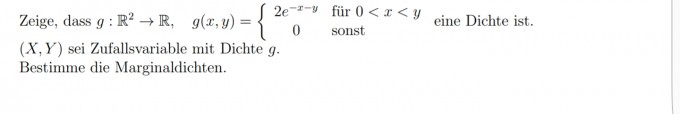
Stochastik Zeigen, dass es sich bei g(x,y) = 2e^{-x-y} für 0<x<y und sonst =0 um eine Dichtefunktion handelt.