Berechnen Sie die maximale Fläche

Question

wie muss ich jetzt vorgehen , ich komme nicht weiter

Comments

"Eine Seite liegt auf der x-Seite" soll das etwa heißen Eine Seite liegt auf der x-Achse ?

Und was ist "einbeschrieben" wenn der Graph nur für 0≤x≤π gegeben ist?

Answer 1

Ich beantworte meine im Kommentar gestellen Fragen einmal selbst und beantworte die ersten zwei Zeilen der Aufgabe, Sei b die Höhe des Rechtecks, dann ist seine Breite π-2sin^-1(b/5) und seine Fläche f(b)=b·[π-2sin-1(b/5)]. Menge der Nullstellen der ersten Ableitung enthält auch das Maximum.

Answer 2

Du kannst dir den ganzen Wust von Informationen
etwas einfacher gestalten. Dann läßt sich
deutlich leichter rechnen.
Stell dir einmal die cos Funktionen vor.
Diese ist eine nach links verschobene
sin Funktion.
f ( x ) = 5 * cos ( x ), Hochpunkt bei x = 0

Die Aufgabenstellung ist dieselbe wie bei deiner
Frage mit f ( x ) = -4x + 5 als Randfunktion.
A ( x ) = x * f ( x )
A ( x ) = x * 5 * cos ( x )
1.Ableitung
A ´( x ) = 5 * ( 1 * cos (x ) + x * -sin(x) )
Extremum

5 * ( 1 * cos (x ) + x * -sin(x) )= 0
Satz vom Nullprodukt anwenden

cos (x ) + x * -sin(x) = 0

cos (x ) - x * sin(x) = 0

cos (x ) = x * sin(x)
1 = x * sin(x) / cos(x)
( sin / cos = tan )
tan ( x ) * x = 1

Über das Newtonverfahren ergibt sich
x = 1.0842

Das Newtonverfahren ist leider etwas schwerer.
Mir fällt leider nichts einfacheres ein.

Das Ergebnis müßte noch auf die Ausgangsfrage
umgerechnet werden.

Hier die Skizze für diese Berechnung.

 

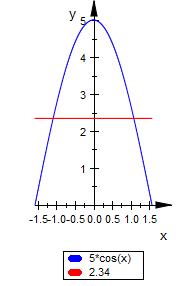
Alle Angaben ohne Gewähr.

Ich will jetzt erst einmal fernsehschauen.

Comments

Über das Newtonverfahren ergibt sich
x = 1.0842

Hast du die Anweisung nicht gelesen "bis sich die fünfte Stelle nach dem Komma nicht mehr ändert" ?
Hier stimmt doch noch nicht einmal die Vorkommastelle.

---

Eventuell x = 0.71046

---

Der richtige Wert ermittelt über das Newton-Verfahren
ist x = 0.86.
Weitere Berechnungen will ich einmal unterlassen
weil es mir komisch vor kommt das Newton-
Verfahren zur Lösung einzusetzen.
Das habt ihr sicherlich noch gar nicht gehabt.

Kann jemand einen einfacheren Weg als
Antwort einstellen ?

Bin bei Bedarf gern weiter behilflich.

---

Aus der Aufgabe: Die notwendige Bedingung für ein mögliches Maximum (kritischer Punkt) ergibt eine Gleichung, die mit dem Newton-Verfahren gelöst werden muss.

---

mit welchem wert muss ich jetzt genau das newton verfahren verwenden?
0.71046 oder 1.0842

x = 0.71 ist für die Ausgangsfrage die
richtige Antwort.

Das Newtonverfahren wurde bereits zur
Lösungsfindung angewendet.

---

x = 0.71 ist für die Ausgangsfrage die
richtige Antwort.
Die fünfte Nachkommastelle ändert sich nicht mehr?

---

Hallo Drasheed,
du hast schon recht viele Fragen eingestellt.
Hast du denn die Antworten verstanden ?
Manche von den Fragen sind nämlich
recht schwer und setzen einiges an Mathe-
kenntnissen voraus.
Geh am besten schrittweise bei deiner Mathe-
weiterbildung vor und versuch erst eine Aufgabe/
Lösung zu verstehen.
Gern helfen wir dir weiter.

Answer 3

A = 5·SIN(x)·(pi - 2·x)

A' = 5·(pi - 2·x)·COS(x) - 10·SIN(x) = 0 --> x = 0.71046

A = 5·SIN(0.71046)·(pi - 2·0.71046) = 5.610963381

Comments

Unsere Antworten sind gleich.
Du hast für die sin-Funktion den x -Wert berechnet.
Ich habe für die von mir angenommene cos-Funktion
den x-Wert berechnet.
Nach Transformation sind beide Werte identisch.

---

mit welchem wert muss ich jetzt genau das newton verfahren verwenden?

0.71046 oder 1.0842

---

Das Newtonverfahren beginnt man nicht mit der Lösung!

Du machst eventuell eine Wertetabelle im Bereich von 0 bis pi in der Schrittweite 0.2 und nimmst dann einen Wert in deren Nähe du eine Nullstelle erwartest.

[0, 15.70796326;
0.2, 11.44802334;
0.4, 6.889564862;
0.6, 2.365903099;
0.8, -1.803371184;
1, -5.330684132;
1.2, -7.976781616;
1.4, -9.564199663;
1.6, -9.987208697;
1.8, -9.217720762;
2, -7.306856759;
2.2, -4.382093391;
2.4, -0.6401360302;
2.6, 3.664116806;
2.8, 8.231950119;
3, 12.73780904]

Ich vermute eine Nullstelle zwischen 0.6 und 0.8 und beginne daher mit x = 0.7.