An welcher Stelle muss der Punkt P liegen, damit der Flächeninhalt A des Rechtecks mit den Eckpunkten Q (0|0), P …

Question

Aufgabe:

Der Punkt P(u|v) liegt auf der Strecke QR mit
Q(0|3) und R (5|0). An welcher Stelle muss der Punkt P liegen, damit der Flächeninhalt A des Rechtecks mit den Eckpunkten Q (0|0), P (ul0), P und P'(0|v) maximal wird?

Problem/Ansatz:

ich verstehe die Aufgabe nicht und habe sie versucht zu jedoch denke Ich benötigt man hier die notwendige bed. und die hinreichende Bed.Kann jemand helfen?

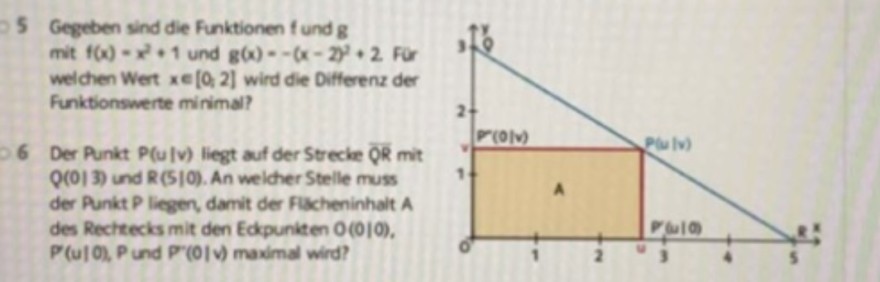
Hier ist meine Aufgabe nochmal visualisiert

Text erkannt:

5 Gegeben sind die Funktionen \( f \) und \( \mathrm{g} \) mit \( f(x)=x^{2}+1 \) und \( g(x)=-(x-2)^{2}+2 \) for welchen Wert \( x \in[0,2] \) wird die Differenz der Funktionswerte minimal?
6 Der Punkt \( P(u \mid v) \) liegt auf der Strecke \( \overline{Q R} \) mit \( Q(0 \mid 3) \) und \( \mathrm{R}(5 \mid 0) \). An welcher Stelle muss der Punkt \( P \) liegen, damit der Fikcheninhait \( A \) des Rechtecks mit den Edpuniten O(0|O), \( P(u \mid 0), P \) und \( P^{\prime}(0 \mid v) \) maximal wird?

Answer 1

Hallo,

bestimme die Gleichung g(x) der Geraden durch Q und R.

P hat die Koordinaten (u | g(u))

Die Hauptbedingung ist also der Flächeninhalt \(A=u\cdot g(u)=u\cdot (-0,6u+3)=-0,6u^2+3u\)

Bilde davon die 1. Ableitung, setze sie = 0 und löse nach u auf. Ich erhalte u = 2,5.

Melde dich, falls noch etwas unklar ist.

Gruß, Silvia

Comments

Dankeschön.Mir ist nichts unklar

MfG Pouamoun

Answer 2

Geradengleichung:

f(x)= mx+b

f(0)= 3

f(5) = 0

m= (0-3)/(5-0) = -3/5

m*0+b = 3

b= 3

f(x)= -3/5*x+3

A=x*f(x) = -3/5*x^2+3

A'(x)= 0

-3/5*x^2 = -3

x^2 =15/3 = 5

x= +-√5, -√5 entfällt

P= (√5/f(√5) = (√5 / -3*√5/5 +3)