
Text erkannt:
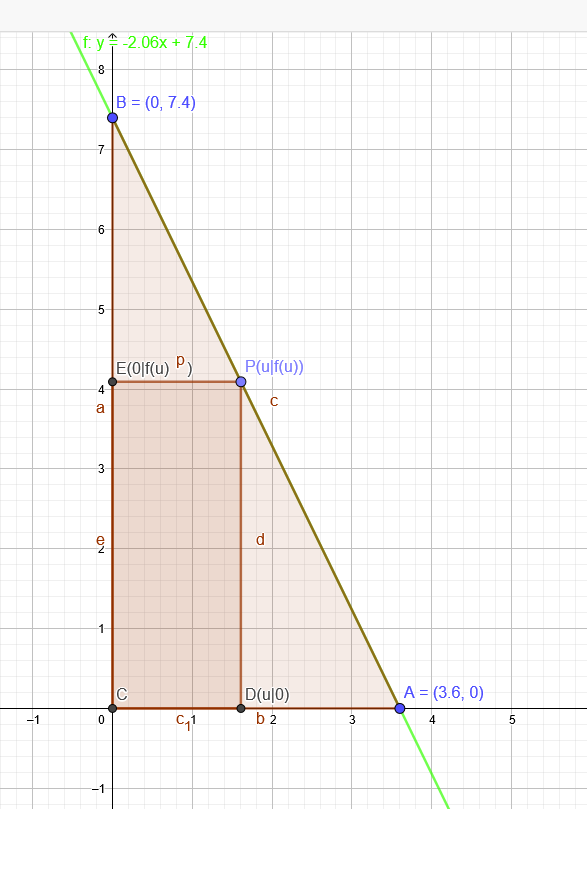
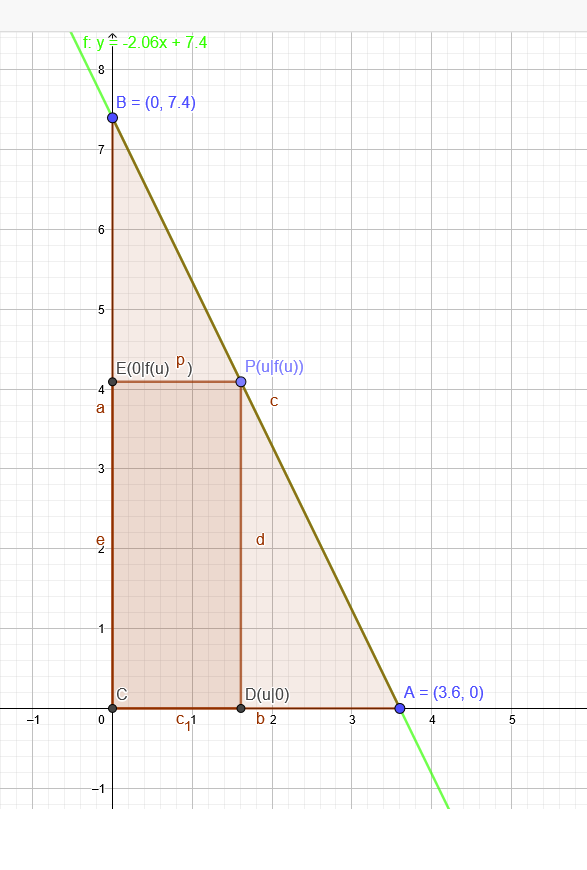
Rechter Winkel im Ursprung: \( C(0 \mid 0) ; A(3,6 \mid 0) \) und \( B(0 \mid 7,4) \)
Gleichung über die 2 -Punkteform der Geraden: \( f(x)=-2,06 x+7,4 \)
\( f(u)=-2,06 u+7,4 \)
\( P(u \mid-2,06 u+7,4) \)
\( A(u)=u \cdot f(u) \) soll maximal werden :
\( A(u)=u \cdot(-2,06 u+7,4)=-2,06 u^{2}+7,4 u \)
\( \frac{d A(u)}{d u}=-4,12 u+7,4 \)
\( \frac{d A(u)}{d u}=0 \)
\( -4,12 u+7,4=0 \)
\( u \approx 1,796 \)
Art des Extremwertes:
\( \left[\frac{d A(u)}{d u}\right] \cdot=-4,12<0 \rightarrow \) Maximum
\( A_{\max } \approx 1,796 \cdot(-2,06 \cdot 1,796+7,4) \approx 6,645 F E \)
\( \mathrm{mfG} \)
Moliets
