Hallo Ruel!
Könnt ihr mir paar Tipps, kleine Erklärung oder eine gute Lernquelle geben?
Eine gute Lernquelle ist das Internet. Ein Tipp ist: Recherchiere im Internet rund um deine Aufgabenstellung und kombiniere möglichst effektiv die Resultate deiner Recherchen, die zum Ergebnis führen! :-O
Wir starten mit der Frage: Wie ändern sich die Koordinaten \( x, z \) eines Vektors \(\vec{v} = \begin{pmatrix}x \\ z \end{pmatrix}\) in der Ebene, wenn er um den Winkel \(\alpha \) gedreht wird? (Daraus lässt sich die Koordinatentransformation um eine beliebige Achse im Raum herleiten. Siehe weiter unten.)
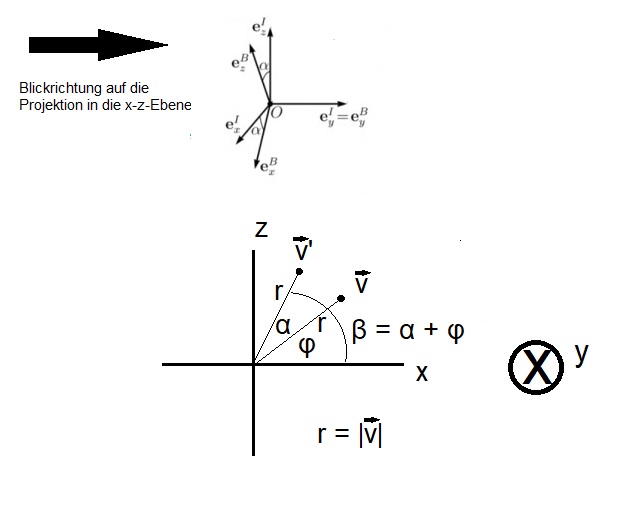
Gesucht sind also die Koodinaten \(x', z' \) des Vektors \(\vec{v'} = \begin{pmatrix}x' \\ z' \end{pmatrix}\), der aus der Drehung des Vektors \(\vec{v} \) um den Winkel \(\alpha \) entsteht.
x = r cos(φ)
z = r sin(φ)
x' = r cos(β)
z' = r sin(β)
β = α + φ
x' = r cos(α + φ)
z' = r sin(α + φ)
Additionstheoreme
sin(α + φ) = sin(α) cos(φ) + cos(α) sin(φ)
cos(α + φ) = cos(α) cos(φ) - sin(α) sin(φ)
x' = r cos(α + φ)
x' = r (cos(α) cos(φ) - sin(α) sin(φ))
x' = r cos(α) cos(φ) - r sin(α) sin(φ))
x' = x cos(α) - z sin(α)
z' = r sin(α + φ)
z' = r (sin(α) cos(φ) + cos(α) sin(φ))
z' = r sin(α) cos(φ) + r cos(α) sin(φ))
z' = x sin(α) + z cos(α)
Durch die Drehung des Vektors \(\vec{v} \) mit den Koordinaten \( x, z \) bekommen wir den Vektor \( \vec{v'} \) und seine Koordinaten \( x', z' \) mit \( x' = x \cdot \cos(α) - z \cdot \sin(α)\) und \(z' = x \cdot \sin(α) + z \cdot\cos(α) \).
Daraus bekommen wir die Drehmatrix A, die den Vektor \(\vec{v} \) in der Ebene um den Winkel \(\alpha \) dreht.
$$A = \begin{pmatrix} a_{11}& a_{12} \\ a_{21} & a_{22} \end{pmatrix}\\A \cdot \begin{pmatrix}x \\ z \end{pmatrix} = \begin{pmatrix}x'\\ z' \end{pmatrix} \\\begin{pmatrix} a_{11}& a_{12} \\ a_{21} & a_{22} \end{pmatrix} \begin{pmatrix}x \\ z \end{pmatrix} = \begin{pmatrix}a_{11}\cdot x + a_{12} \cdot z\\a_{21}\cdot x + a_{22} \cdot z\end{pmatrix} = \begin{pmatrix} x \cdot \cos(α) - z \cdot \sin(α) \\x \cdot \sin(α) + z\cdot \cos(α)\end{pmatrix}\\\Rightarrow a_{11} = \cos(α), ~ a_{12} = - \sin(\alpha), ~ a_{21}=\sin(\alpha), ~ a_{22} = \cos(\alpha) \\\Rightarrow A = \begin{pmatrix} \cos(α) & - \sin(\alpha) \\ \sin(α) & \cos(\alpha) \end{pmatrix} $$
Für einen eher intuitiven Zugang zur Drehmatrix ohne Additionstheoreme guckst du z.B. hier
Das Resultat (ohne Additionstheoreme) genügt dann auch für die folgende Fortsetzung.
Multiplizieren wir also die Matrix \(A \) mit einem Vektor \(\vec{v} \), erhalten einen Vektor \(\vec{v'} \), der um den Winkel \(\alpha \) gedreht ist. Das wussten wir aber schon vorher(*), denn wir haben ja schon die entsprechenden Gleichungen hergeleitet:
x' = x cos(α) - z sin(α) und
z' = x sin(α) + z cos(α). (Das gilt in der Ebene - egal ob die Achsen x, z oder sonstwie heißen. )
(*)
Du kannst dir entweder die Gleichungen oder die Drehmatrix A merken bzw. in deine Formelsammlung schreiben. Die Matrix A kann man sich vlt. einfacher als die Gleichungen merken.
Mit Hilfe dieser Gleichungen in der Ebene(bzw. der Drehmatrix A) können wir uns überlegen, wie eine Drehmatrix \( D\) aussehen muss, die einen Vektor \(\vec{v} \) im Raum um eine beliebige Achse dreht. Der Aufgabenstellung wegen wählen wir zweckmäßigerweise die y-Achse, um die wir einen Vektor \(\vec{v} \) drehen wollen.
Wir suchen also zunächst die Matrix \(D \), die einen Vektor \(\vec{v} \) um die y-Achse dreht. Dann gilt \(D\cdot \vec{v} = \vec{v'} \)
$$D \cdot \vec{v}=\begin{pmatrix}a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix}\begin{pmatrix} x \\ y \\ z \end{pmatrix} =\begin{pmatrix} x' \\ y' \\ z' \end{pmatrix} = \begin{pmatrix}a_{11}\cdot x + a_{12}\cdot y + a_{13}\cdot z \\ a_{21}\cdot x + a_{22}\cdot y + a_{23}\cdot z \\ a_{31}\cdot x + a_{32}\cdot y + a_{33}\cdot z \end{pmatrix} $$
Aus unseren Gleichungen und aus der Vorgabe \( y' = y \) der Aufgabenstellung folgen die Einträge \(a_{ij} \) der Matrix \(D \):
$$ x' = x \cdot \cos(α) - z\cdot \sin(α) \Rightarrow a_{11}=\cos(α)\ a_{12}=0 ~ a_{13} = -\sin(\alpha) \\y' = y \Rightarrow a_{21} = 0, ~ a_{22} = 1, ~ a_{23} = 0\\z' = x\cdot \sin(α) + z\cdot \cos(α) \Rightarrow a_{31} = \sin(\alpha), ~ a_{32}=0, ~ a_{32} = \cos(\alpha) $$
Unsere Drehmatrix \(D \), die einen Vektor um den Winkel \(\alpha \) dreht, ist damit fertig, wir brauchen nur noch die \(a_{ij} \) einzusetzen: $$ D = \begin{pmatrix} \cos(α)& 0 & -\sin(\alpha) \\ 0 & 1 & 0 \\ \sin(\alpha) & 0 & cos(\alpha) \end{pmatrix}.$$
Obiges ist die Drehmatrix für eine aktive Drehung(Vektor wird gedreht). Wir brauchen eine Drehmatrix für eine passive Drehung(Koordinatentransformation).
Vgl aktive vs. passive Drehung z.B. hier https://www.mathebibel.de/drehmatrix
Das wird gleich der leichteste Teil vom Ganzen. Wir brauchen nur noch die Transponierte der Matrix \(D \).
Dann gilt \( A_{BI} = D^T \) und damit
$$A_{BI} = \begin{pmatrix} \cos(α)& 0 & \sin(\alpha) \\ 0 & 1 & 0 \\ -\sin(\alpha) & 0 & cos(\alpha) \end{pmatrix}.$$
Probe
1)
Drehen wir den Vektor(aktive Drehung) \( \vec{v} = \begin{pmatrix}1 \\ 0 \\ 0\end{pmatrix} \) um die y-Achse und wählen den Drehwinkel \(\alpha = 90° \) müssten wir den Vektor \( \vec{v'} = \begin{pmatrix} 0\\ 0\\ 1\end{pmatrix} \) bekommen. D.h. es müsste \(D\cdot \begin{pmatrix}1 \\ 0 \\ 0\end{pmatrix} = \begin{pmatrix} 0\\ 0\\ 1\end{pmatrix} \) gelten.
2)
Lassen wir den Vektor wo er ist und drehen das Koordinatensystem(passive Drehung), müssten wir \(\vec{v'} = \begin{pmatrix} 0 \\ 0 \\ -1 \end{pmatrix} \) erhalten, d.h. als Ergebnis häten wir gern \(A_{BI}\cdot \begin{pmatrix}1 \\ 0 \\ 0\end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ -1 \end{pmatrix}\)
Wir rechnen nach, oder lassen rechnen
https://www.wolframalpha.com/input/?i=%7B%7Bcos(90%C2%B0),+0,+-sin(90%C2%B0)%7D,+%7B0,+1,+0%7D,+%7Bsin(90%C2%B0),+0,+cos(90%C2%B0)%7D%7D.%7B%7B1%7D,%7B0%7D,%7B0%7D%7D
https://www.wolframalpha.com/input/?i=%7B%7Bcos(90%C2%B0),+0,+sin(90%C2%B0)%7D,+%7B0,+1,+0%7D,+%7B-sin(90%C2%B0),+0,+cos(90%C2%B0)%7D%7D.%7B%7B1%7D,%7B0%7D,%7B0%7D%7D
Der Vergleich der Ergebnisse mit unseren Wunschergebnissen, die wir uns logisch erschlossen haben, scheinen erfolgversprechend zu sein ==> Jippieee!!! :-)
Demnach sollten unsere Überlegungen für beliebige Winkel α gelten.
Viel Erfolg!
Grüße