Hier eine Lösung als Berechnung
Gegeben : die Koordinaten der 3 Eckpunkte.
Das Dreieck wird in ein Koordinatenkreuz
eingepaßt. Ein Eckpunkt in den Koordinatenursprung,
die gegenüberliegende Seite parallel zur y-Achse.
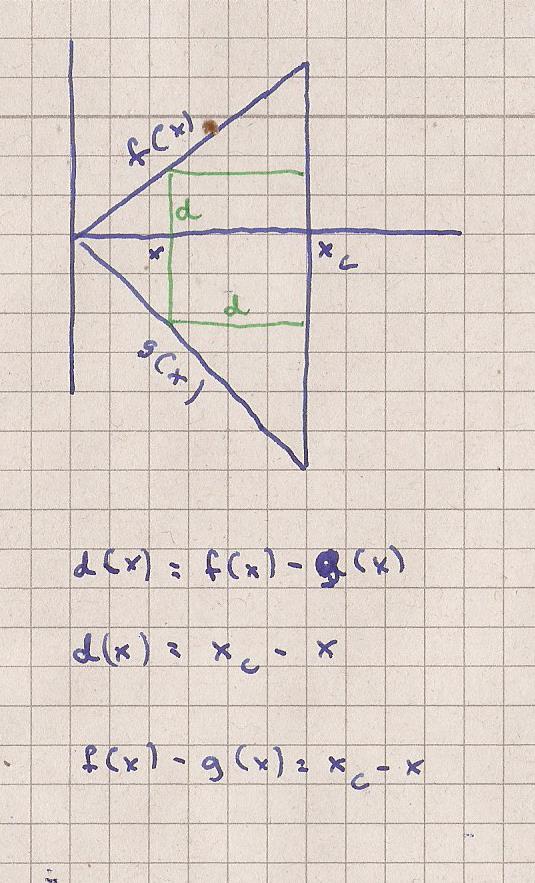
Es werden die schräglaufenden Seiten des Dreiecks
als Geraden berechnet. f(x) und g(x).
Die Differenzfunktion ist d ( x ) = f ( x ) - g ( x ).
d ist die Seite gesuchten Quadrats.
Das andere d ist x(c) - x.
x ( c ) ist fest.
f ( x ) - g ( x ). = x(c) - x
Ob es einfacher geht weiß ich nicht.
Gegeben : die Koordinaten der 3 Eckpunkte.
Gesucht : Länge der Quadratseite