Integration: Wie berechnet man den Flächeninhalt?

Question

Aufgabe 14 b): Wie groß ist der Inhalt der markierten Fläche? Die drei gegebenen Graphen sind eine Gerade, eine Normalparabel und eine verschobene Normalparabel.

Comments

Vom Duplikat:

Titel: Anwendungen der Integralrechnung

Stichworte: integral,fläche,graphen

Aufgabe:

A wird durch eine Gerade und zwei Kurven eingeschlossen. Im ersten Schritt müssen die Gleichungen dieser Funktionen bestimmt werden.

Problem/Ansatz:

Ich meine alles soweit verstanden zu haben, und habe für A ≈ 1.8 raus. Die Aufgabe scheint hier schon zu existieren, hat aber ein anderes Ergebnis als Antwort, nämlich A = 1.3 (ist schon älter)  https://www.mathelounge.de/50386/integration-wie-berechnet-man-den-flacheninhalt

Daher wollte ich Fragen ob das Ergebnis jemand überprüfen könnte

Meine Funktionsgleichungen sind

f(x) = 2x + 2

g(x) = x^2

h(x) = x^2 - 2x + 2

Answer 1

die Funktionsgleichungen stimmen.

Ich komme auch auf ungefähr 1.8: 
$$A=\int_{1-\sqrt{3}}^{0}\left [(2x+2)-(x^2)\right]dx + \int_{0}^{1}\left [(x^2-2x+2)-(x^2) \right ] dx \\ = \int_{1-\sqrt{3}}^{0}\left [(2x+2)-(x^2)\right]dx + 1 \approx 1.798$$

Comments

Okay, ich war nur etwas irritiert von der Frage im anderen Thread und der Antwort, weil ja die Aufgabe dieselbe zu sein scheint

---

Ja, die Frage ist auch identisch. Man hat sich dort nur verrechnet.

Hier nochmal grafisch dargestellt:

https://www.geogebra.org/m/yys6txta

Answer 2

Hi

14 b) Gesucht ist die Fläche, die von den beiden Parabeln und der Geraden eingeschlossen wird.

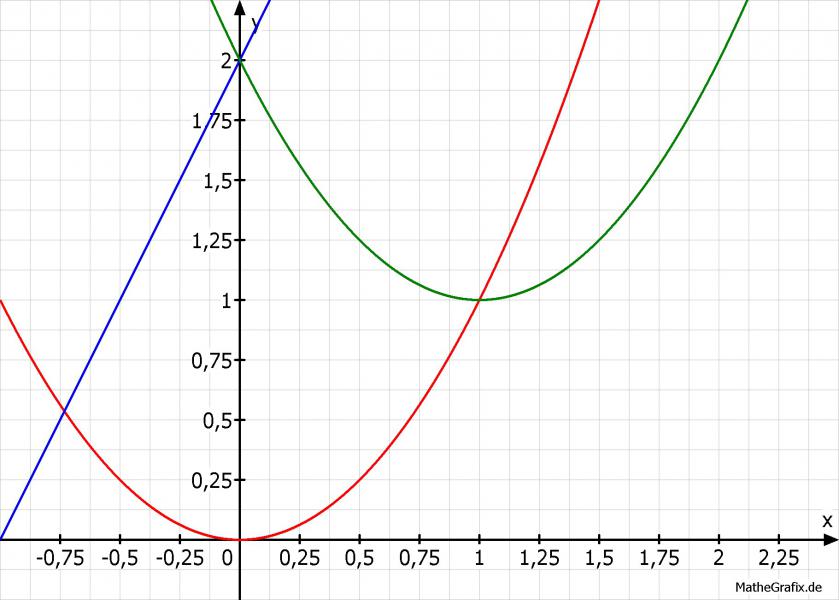
Funktionsgleichungen für die Funktionen p, q und g: p(x) = x^2     q(x) = (x-1)^2+1     g(x) = 2x+2

p(x) = x^2; Normalparabel, Scheitel im Nullpunkt

q(x) = (x-1)^2+1; verschobene Normalparabel, Scheitel bei (1|1)

g(x) = 2x+2; Gerade mit Steigung 2 und Schnittpunkt mit der y-Achse bei (0|1)

(Falls es Fragen zum erstellen der Gleichungen gibt → Kommentar)

x-Werte der Schnittpunkte der Kurven für die Integrationsgrenzen:

p(x) = g(x);

x^2 = 2x+2;

x^2 -2x -2 = 0; | quadratische Gleichung liefert

x1 = 1-sqrt(3);   x2 = 1+sqrt(3);  | x2 ist nicht weiter interessant

x3 = 0; | kann und darf aus Zeichung abgelesen werden, gemäß Aufgabenstellung

x4 = 1;

Flächenberechnung mittels Integration:

F = ∫_x1⁰g(x) dx + ∫₀^x4q(x) dx - ∫_x1^x4p(x) dx; | Integrieren, Grenzen einsetzen (ist sehr aufwendig aufzuschreiben daher nur auf Anfrage → Kommentar)

F ≈ 1.798

 EDIT(Lu) 2018. Vgl. Diskussion 2018.

Bei Fragen, Fehlern oder Anmerkungen → Kommentar

lg JR

Comments

Ich komme da nicht weiter könntest du wenn du zeit hast den ganzen Rechenfehler aufschreiben ? :)

---

deine Lösung stimmt leider nicht. Du hast dich bei den Integrationsgrenzen vertan. Richtig wäre \(x_1=1-\sqrt{3}\) und nicht \(\sqrt{5}\).

Dieser "kleine" Unterschied verkleinert A um \(\approx 0.48 \textrm{FE}\).

Hier wurde das gleiche Thema nochmal diskutiert: https://www.mathelounge.de/598182/

---

EDIT: Habe das nun in der Antwort korrigiert. Danke für die Hinweise.

Answer 3

Die drei Funktionsgleichungen sind richtig.

Der Teil der Fläche, der im ersten Quadranten liegt, hat (auch ohne Integralrechnung) exakt den Flächeninhalt 1.

Konzentriere dich nun auf das Stück im 2. Quadranten.

Comments

Und das Ergebnis der Fläche ? :D

---

Gegenfrage: An welcher (für deine Integration wichtigen) Stelle schneiden sich Gerade und Normalparabel?