Aufgabe:
Gegeben seien die Funktionen f(x)=4x^3+x^2-9x und g(x)=0,5x^2+4.
Berechnen Sie die Fläche, die von den beiden Graphen f und g eingeschlossen wird.
Problem/Ansatz:
Ich denke ich muss zunächst die x-Werte der Schnittpunkte bestimmen indem ich f(x)=g(x) gleichsetze. Dabei bekomme ich die Werte x1=-1,27; x2=-0,48; x3=1,63 raus. Jetzt muss ich herausfinden, welcher der Graphen höher liegt, weshalb ich einmal einen Wert zwischen -1,27 und -0,48 einsetze und einmal zwischen -0,48 und 1,63.
f(-1)=6 > g(-1)=4,5 –> Im Intervall [-1,27;-0,48] ist f(x) größer als g(x)
f(1)=-4 < g(1)=4,5 –> Im Intervall [-0,48;1,63] ist g(x) größer als f(x)
Jetzt bilde ich also Integrale und berechne: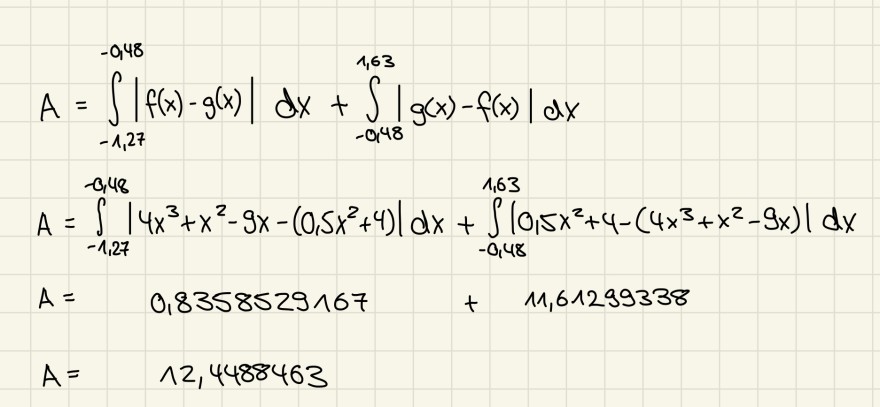
Text erkannt:
\( \begin{array}{l}A=\int \limits_{-1,27}^{-0,48}|f(x)-g(x)| d x+\int \limits_{-0,48}^{1,63}|g(x)-f(x)| d x \\ A=\int \limits_{-1,27}^{-0,48}\left|4 x^{3}+x^{2}-9 x-\left(0,5 x^{2}+4\right)\right| d x+\int \limits_{-0,48}^{1,63}\left|0,5 x^{2}+4-\left(4 x^{3}+x^{2}-9 x\right)\right| d x \\ A=\quad 0,8358529167+11,61299338 \\ A=\quad 12,4488463\end{array} \)
Habe ich das richtig gemacht?