Flächeninhalt zwischen zwei Graphen berechnen

Question

Ich habe folgende Aufgabe berechnet:

Gesucht ist der Inhalt der Fläche, welche von den Graphen der Funktionen f(x) = x und g(x) = 1/4x^2 - 1/2x eingeschlossen wird.

Ich habe zunächst einmal die Schnittpunkte für das Intervall berechnet:

x₁ = 0, x₂ = 6

I = [1;6]

Danach habe ich die Differenzfunktion von f(x) und g(x) ausgerechnet:

h(x) = 1/4x^2 + 3/2x

Anschließend habe ich die Fläche mit h(x) berechnet:

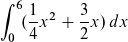
Daraus ergibt sich dann für A = 45

Ist das richtig?

MfG

Answer 1

Deine differenzfunktion ist falsch. Es muss 1/4x^2-3/2x heißen. Also Lösung kommt 9 heraus.

Comments

Hallo Kofi,
bei deiner Funktion ( g minus f ) kommt -9
heraus.

---

f(x) - g(x) = x - (1/4x^2 - 1/2x)

x - (-1/2x) = 3/2x, weil - - gleich + ergibt.

Oder habe ich einen falschen Gedankengang?

---

Georg hast recht. Für mich ist der flächeninhalt 9.

@Falabella: du hast recht es sind 3/2x. Dann müssen es aber -1/4x^2 sein. Du hast das minus vergessen.

Answer 2

f(x) = x ( blau ) und
g(x) = 1/4x2 - 1/2x ( rot )

Intuitiv würde man bei der Flächenermittlung
die unter Funktion von der oberen Funktion
abziehen ( f - g ) , dann würde die Fläche direkt
positiv herauskommen.
Dies ist aber nicht notwendig. man kann auch
f von g abziehen. Sollte einmal ein Wert bei der
Flächenberechnung negativ herauskommen
wird er einfach postiv gesetzt.
Flächen sind immer positiv.