Vektoren im Raum - Gleichungssystem mit 6 Unbekannten

Question

ich sitze an folgender Aufgabe:

"Geben Sie Werte für die Variablen a, b, c und d an, sodass die Geraden g: $$ \xrightarrow { x } =\begin{matrix} -5 \\ 7 \\ a \end{matrix}+\quad r\begin{matrix} b \\ -6 \\ 2 \end{matrix} $$ und h: $$ \xrightarrow { x } =\begin{matrix} 1 \\ c \\ 3 \end{matrix}+\quad s\begin{matrix} -3 \\ 3 \\ d \end{matrix} $$ sich schneiden.

Ich habe folgendes gerechnet:

 

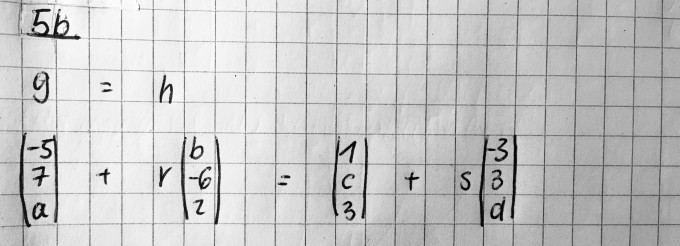
Jetzt ist meine Frage : Dadurch, dass es ja mehr Unbekannte gibt als Gleichungen, gibt es ja mehrere mögliche Lösungen. Drei Unbekannte kann man ja dann wählen, ich habe s null gesetzt, damit gleich eine weitere Unbekannte wegfällt. Jetzt bin ich mir aber unsicher, ob die Probe so richtig ist. Ich hatte ersucht mit GeoGebra das graphisch zu überprüfen, bin aber als Laie kläglich gescheitert :)

Wie kann ich herausfinden, ob mein Ergebnis stimmt oder nicht?

Comments

Wenn du den Schnittpunkt noch ausrechnest, kannst du alles hier einzeichnen und dann solltest du beurteilen können, ob dein Resultat stimmt. 

https://www.matheretter.de/geoservant/de

---

Der Link scheint nicht zu funktionieren :(

---

Jetzt? 

Habe einen Leerschlag vor dem Zeilenumbruch entfernt. Kann sein, dass der Editor das nicht mag. 

---

Danke, jetzt geht es, aber ich bekomme es irgendwie nicht hin. Da ist ja nur eine Funktion zum Vektoren eintragen, bin mir da ziemlich unsicher, weil ich habe das ja alles schick in Parameterform. Als Schnittpunkt habe ich wie oben in der Probe (1|1|3) :)

Answer 1

Ich habe jetzt mit s=t=1 jeweils einen zweiten Punkt auf den Geraden ausgerechnet. Da kommt dann dein Schnittpunkt bereits vor und alles sieht gut aus:

https://www.matheretter.de/geoservant/de?draw=gerade(-5%7C7%7C1%201%7C1%7C3)%0Agerade(1%7C1%7C3%20-2%7C4%7C3)%0Apunkt(1%7C1%7C3%20%22P%22)

Wie du gesagt hast, ist das jetzt einfach EINE Lösung. Es dürfte viele Lösungen geben.

Mit Hilfe von Vektoren und Beschriftungen noch etwas ausgeschmückte Zeichnung:

https://www.matheretter.de/geoservant/de?draw=gerade(-5%7C7%7C1%201%7C1%7C3)%0Agerade(1%7C1%7C3%20-2%7C4%7C3)%0Apunkt(1%7C1%7C3%20%22P%22)%0Avektor(-5%7C7%7C1%206%7C-6%7C2)%0Avektor(1%7C1%7C3%20-3%7C3%7C0)%0Apunkt(-5%7C7%7C1%20%22A%22)%0Apunkt(1%7C1%7C3%20%22B%22)

Answer 2

Tatsächlich kann man 3 Variable vorgeben und dann die anderen 3 berechnen. Wenn man zum Beispiel a, b und r vorgibt, dann wählt man auf diese Weise unter der ersten Geradenschaar eine bestimmte aus. Wähle z.B.a=1,b=0 und r=3. Dann gilt

(1) -5=1- 3s und folglich s=2

(2) 7 -18= c + 6 und folglich c=-17

(3) 1+ 6 = 3 + 2d und folglich d=2

Damit sind alle Variablen so gewählt, dass die Geraden sich schneiden.