Hallo probe,
Du fragst "Wo findet man den Winkel alpha in der Skizze wieder?" So ziemlich überall:
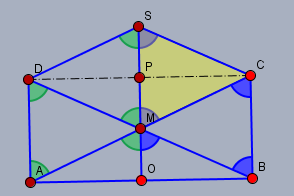
Ich unterstelle, dass alle vertikalen Linien zueinander parallel laufen sollen und senkrecht auf der Grundlinie \(AB\) stehen. \(P\) sei der Schnittpunkt der Strecken \(CD\) und \(OS\). Da die Abstände der beiden äußeren Vertikalen zur mittleren Vertikalen gleich sind, teilt \(AC\) die Strecke \(OP\) in \(M\) zur Hälfte. Demnach sind \(MP\) und \(PS\) beide \(=a/2\) und damit gleich lang. Da \(PC\) parallel zu \(AB\) und damit senkrecht zu \(MS\) verläuft, ist das Dreieck \(MSC\) ein gleichschenkliges mit den Schenkeln \(MC\) und \(SC\). Und den gleiche großen Basiswinkeln \(\angle CMS\) und \(\angle MSC=\alpha\).
\(\angle CMS\) und \(\angle MCB\) sind Wechselwinkel an Parallelen und damit auch gleich. Wegen der Symmetrie ist das Dreieck \(BCM\) ebenfalls gleichschenklig mit den Basiswinkeln \(\angle CBM\) und \(\angle MCB\). \(\angle OMB\) ist Wechselwinkel zu \(\angle CBM\).
Also sind alle blau markierten gleich groß bzw. \(= \alpha\). Die grünen Winkel sind ebenfalls \(=\alpha\), da die Figur symmetrisch zur Achse durch \(OS\) ist.
Gruß Werner
Edit: Winkeldrehrichtung korrigiert