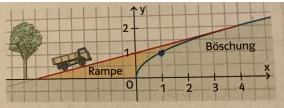
Aufgabe:
Das Profil einer Böschung wird durch den Graphen der Funktion f mit \( f(x)=\sqrt{x} \) beschrieben.
a) Berechnen Sie den Steigungswinkel der Böschung in \( B_{1} (1|1) \) und \( B_{2}(9|3) \).
b) An die Böschung wird eine Rampe mit Steigungswinkel 14° gebaut, die im Punkt \( B(1|1) \) an der Böschung endet. Begünnden Sie, dass diese Rampe nicht knickfrei an der Böschung endet. Wo beginnt diese Rampe und wie lang wird sie?
c) An die Böschung soll eine Rampe mit 14° Steigung knickfrei angebaut werden. Wo beginnt die Rampe an der Böschung und wie lang wird sie?