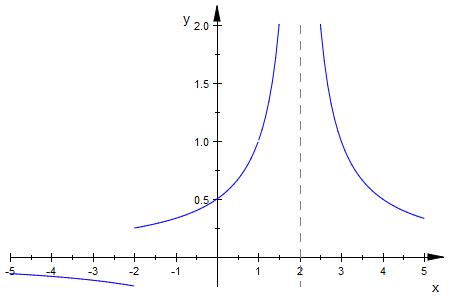
f(x) = (x^2 +x-2) / ( abs ( x^2 - 4 ) * (x-1))
a) den maximal möglichen Definitionsbereich
Nenner = 0, Division ausschließen
abs ( x^2 - 4 ) * (x-1) = 0
Satz vom Nullprodukt anwenden
abs ( x^2 - 4 ) = 0
x^2 - 4 = 0
x^2 = 4
x = +2
und
x = -2
x -1 = 0
x = 1
D = ℝ \ { -2; 1 ; 2 }
b) untersuchen Sie das Verhalten an den
Definitionslücken
c) und bilden Sie die Grenzwerte lim
x→∞
f(x) sowie lim
x→−∞
f(x) .
b.) + c.) kommen noch
d) Fertigen Sie abschließend eine Skizze des Funktionsgraphen an.