Hi
Ich hab' mal versucht die Aufgabe zu rekonstruieren.
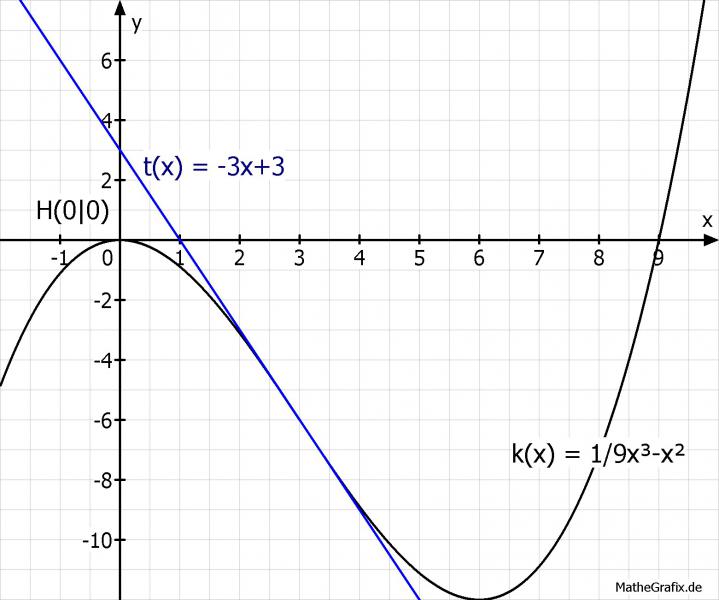
Erstmal die Ableitungen bilden:
f(x) = ax^3 +bx^2 +cx +d;
f'(x) = 3ax^2 +2bx +c;
f''(x) = 6ax +2b;
f'''(x) = 6a;
Dann bestimmst Du die Parameter der Funktion, die den Kanal beschreibt:
(1) f(x=0) = 0 = d;
(2) f'(x=0) = 0 = c;
(3) f(x=9) = 0 = 729a +81b;
(4) f'(x=6) = 0 = 108a +12b; // linear abhängig von (3)
(5) f''(x=3) = 0 = 18a +2b; // linear abhängig von (3) und (4)
-> b = -9a; a und b freiwählbar. Da aber ein Kanal entstehen soll (oder zumindest etwas das so ähnlich aussieht) und der Beobachtungspunkt über H(0|0) liegt, habe ich mal für a = 1/9 und für b = -1 gewählt.
-> f(x) = 1/9*x^3 -x^2
Damit man vom Beobachtungspunkt B aus auch alles vom Kanal sehen kann muss der Blickwinkel mindestens so steil sein wie die größte Steigung der Kanalwand. Der Punkt größter Steigung ist der Wendepunkt (Anmerkung: Die Ableitung f' einer Funktion f von x liefert die Steigung dieser Funktion an der Stelle x. Die zweite Ableitung f'' liefert also die Steigung von f' an der Stelle x. Wenn man eine Ableitung Null setzt kann man die x-Werte der Extrema der ursprünglichen Funktion bestimmen. Wenn man nun f'' = 0 setzt, dann erhält man die Orte der Extrema von f' und damit die Orte mit der größten Steigung).
Der Schnittpunkt der Tangenten an die Funktion f durch den Wendepunkt mit der y-Achse liefert den Beobachtungspunkt B.
Steigung der Wendetangente:
f'(x=3) = -3;
WP bestimmen:
f(x=3) = -6; -> WP(3 | 9);
Wendetangente, Parameterbestimmung durch einsetzen der Steigung und des WP:
t(x) = -3x +3;
Schnittpunkt mit der y-Achse:
t(x=0) = 3; -> B(0 | 3)
Der Kanal ist also ab einer Höhe größer als 3 vollständig einsehbar.
Ich hoffe mal, dass das in etwa Deine Aufgabe war. Wenn nicht --> Kommentar
lg JR