Integralrechnung-parabel 4. ordnung

Question

Eine zur y.Achse symmetrischen Parabel 4.Ordnung, die zwei Nullstellen hat, schneidet die x-Achse bei x=4, die y-Achse bei y=2 und schliesst mit der x.Achse eine Fläche vom Inhalt A=44.8 ein.

Bestimme die Parabelgelcihung (Lösung: -1/8(x⁴-15x²-16)

Ich komme gar nicht draus, ausser das eine y Achse symmetrische Parabel = ax⁴+bx²+c ist. Und dass c=2 ist.

Answer 1

Eine zur y.Achse symmetrischen Parabel 4.Ordnung, die zwei Nullstellen hat, schneidet die x-Achse bei x=4, die y-Achse bei y=2 und schliesst mit der x.Achse eine Fläche vom Inhalt A=44.8 ein.

f ( x ) = a * x^4 +b * x^2 + 2

f ( 4 ) = a * 4^4 + b *  4^2 + 2 = 0
f ( 4 ) = 256a  + 16b + 2 = 0

Stammfunktion
S ( x ) = a * x^5 / 5 + b * x^3 / 3 + 2 * x
Flächeninhalt im 1.Quadranten
[ S ( x ) ] zwischen 0 und 4 ist 22.4

a * 4^5 / 5 + b * 4^3 / 3 + 2 * 4 = 22.4

1024/5 * a + 64/3 * b + 8 = 22.4
und
256a  + 16b + 2 = 0

2 Gleichungen mit 2 Unbekannten

a = -0.125
b = 1.875

Alle Angaben ohne Gewähr.
Bitte nachrechnen und die Probe machen.
Bin bei Bedarf gern weiter behilflich.

Answer 2

Guten Abend! :-)

Der Ansatz $$a\cdot\int \limits_{-4}^{+4}{\left(\left(x^2-4^4\right)\cdot\left(x^2+1\right)\right)\textrm{d}x}=44,8$$der sich für eine händische Rechnung noch mehrfach vereinfachen lässt, liefert schnell den noch benötigten Faktor \(a=-\dfrac{1}{8}.\)

Answer 3

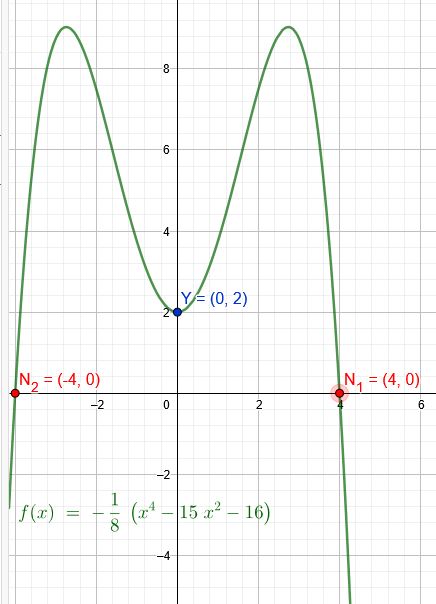
Eine zur y-Achse symmetrischen Parabel 4.Ordnung, die zwei Nullstellen hat, schneidet die x-Achse bei \(x=4\), die y-Achse bei \(y=2\) und schließt mit der x-Achse eine Fläche vom Inhalt \(A=44,8\) ein.

\(f(x)=a(x-4)(x+4)(x-N)(x+N)\\=a(x^2-16)(x^2-N^2)\\=a(x^4-N^2x^2-16x^2+16N^2)\)

\(\frac{22,4}{a}=\int\limits_{0}^{4}(x^4-N^2x^2-16x^2+16N^2)dx\\=[\frac{1}{5}x^5-\frac{N^2}{3}x^3-\frac{16}{3}x^3+16N^2x ]_{0}^{4}\\=[\frac{1}{5} \cdot4^5-\frac{N^2}{3}\cdot 4^3-\frac{16}{3}\cdot 4^3+64N^2]-0\\=[204,8-341,3333333-21,33333333N^2+64N^2]\\=[-136,533333+42,66666667N^2] \)

\(a=\frac{22,4}{42,66666667N^2-136,533333}\) :

\(f(x)=\frac{22,4}{42,66666667N^2-136,533333}(x^4-N^2x^2-16x^2+16N^2)\)

Y\((0|2)\)  :

\(f(0)=\frac{22,4}{42,66666667N^2-136,533333}\cdot 16N^2=2\)

\(\frac{179,2N^2}{42,66666667N^2-136,533333}=1\)

\(179,2N^2=42,66666667N^2-136,533333\)

\(179,2N^2-42,66666667N^2=-136,533333\)

\(N^2=-1\):

\(a=\frac{22,4}{-42,66666667-136,533333}=-0,125\) :

\(f(x)=-0,125(x^4-15x^2-16)\)

Comments

Ich empfehle NIEMANDEM, solche schönen Brüche in Dezimalzahlen umzurechnen! Und dann werden auch noch willkürlich viele Nachkommastellen gewählt. Mal sechs, mal sieben, mal acht... Einfach nur sehr schlechter Stil. Bitte nicht nachmachen!

---

Ich habe die Werte per Excel berechnet und dann übertragen. In der Regel mag ich auch lieber Brüche.