Integralrechnung + Parabel + Geraden f(x)=x²; g:y=; A=36FE

Question

 

und zwar komme ich kein Stück bei folgender Aufgabe weiter, ich denke bestimmt wieder viel zu kompliziert.

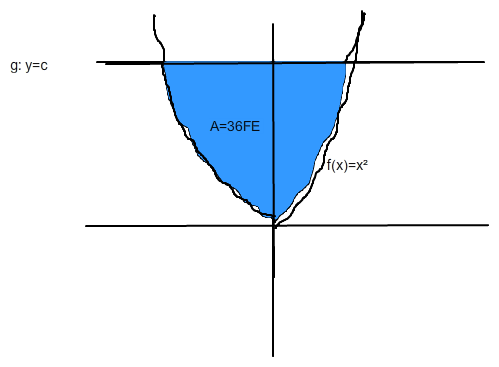
Welche der Geraden g: y=c schließt mit der Parabel zu f(x) = x² eine Fläche mit 36FE ein?

Ich habe auch eine Skizze von der Aufgabe die mir alles anzeigt, nur krieg ich es nicht in einem ordentlichen Zusammenhang gebracht.

also F(x)= 1/3 x³ + C und es müsste ja achsensymmetrisch sein, dass heißt ax² + C. Aber ich komm einfach nicht mehr weiter.

Sorr für die schlechte Zeichnung habe nur einen Laptop ohne seperate Maus ;)

 

Answer 1

Leichter ist es wenn man sich das ganze dreht und somit die Wurzelfunktion betrachtet.

f(x) = √x = x^{1/2}

F(x) = 2/3·x^{3/2} = 36/2

x = 9

Also lautet die Gleichung y = 9

Skizze

Comments

Also jetzt bin ich noch etwas mehr verwirrt.

Weil wie kommt man auf x^1/2 weil wenn ich doch aus x^1 die Wurzel ziehe bleibt doch das Ergebnis gleich.

---

Wenn du aus 9 die Wurzel ziehst bleibt das Ergebnis doch nicht gleich.

---

Nein, dass meinte ich auch nicht aber du hast ja den Ansatz f(x) = √x = x1/2 geschrieben und den kann ich nicht nachvollziehen.

---

Zeichne dir mal die Funktion y = x^2 in ein Koordinatensystem und dann die Funktion y = √x. Ich hoffe dir fällt dann etwas auf.