Parabel 3. Ordnung berechnen (mit Berührungs- und Schnittpunkt sowie Fläche)

Question

Ich bin aufgeschmissen. Folgende Aufgabe:
Eine Parabel 3. Ordnung schneidet die Parabel p: y=(x-2)² bei x=0 und berührt sie bei x=2. Die beiden Parabeln schliessen im 1. Quadranten eine Fläche vom Inhalt A=4 ein. Bestimme die Gleichung der Parabel 3. Ordnung.
Nun, bis jetzt habe ich folgendes:
q: y=ax³+bx²+cx+d 
1) q'(2)=p'(2) --> 12a+4b+c=0
2) q(0)=p(0) --> d=4   
3)  Betrag von ∫_xo^x1((ax³+bx²+cx+d)-(x-2)²)dx =4   
Stimmt das? Was soll ich tun....

Answer 1

Eine Parabel 3. Ordnung schneidet die Parabel p: y=(x-2)² bei x=0
und berührt sie bei x=2. Die beiden Parabeln schliessen im
1. Quadranten eine Fläche vom Inhalt A=4 ein. Bestimme
die Gleichung der Parabel 3. Ordnung.

f ( x ) = a*x^3 + b*x^2 + c* x + d
p ( x ) = x^2 - 4x + 4

p ( 0 ) = 4
p ( 2 ) = 0
p ´( x ) = 2x - 4 ;
p ´ ( 2 ) = 0

f ´( x ) = 3a*x^2 + 2b*x + c

f ( 0 ) = d = 4  => d = 4
f ( 2 ) = a*2^3 + b*2^2 + c* 2 + 4 = 0
8a  + 4b + 2c + 4 = 0

p ´( 2 ) = f ´( 2 ) = 0
3a*2^2 + 2b*2 + c = 0 
12a + 4b + c = 0
8a  + 4b + 2c + 4 = 0

a*x^3 + b*x^2 + c* x + 4 - ( x^2 - 4x + 4 )
a*x^3 + b*x^2 + c* x + 4 - x^2 + 4x - 4
a*x^3   + b*x^2 + c * x - x^2 + 4x
∫ a*x^3   + b*x^2 + c * x - x^2 + 4x dx
a*x^4/4 + b*x^3/3 + c*x^2 /2 - x^3/3 + 2x^2
[ a*x^4/4 + b*x^3/3 + c*x^2 /2 - x^3/3 + 2x^2 ]₀²

12a + 4b + c = 0
8a  + 4b + 2c + 4 = 0
a*2^4/4 + b*2^3/3 + c*2^2 /2 - 2^3/3 + 2*2^2 = 4

Damit hätten 3 Gleichungen mit 3 Unbekannten.
Sollte lösbar sein.
23:06 Uhr. Ist es schon spät.
Ich hoffe ich konnte dir weiterhelfen.

Alle Angaben ohne Gewähr.

Comments

a = 3
b = -11
c = 8
d = 4

f ( x ) = 3 *x³ + (-11)*x² + 8* x + 4
p ( x ) = x² - 4x + 4 

Eine Parabel 3. Ordnung schneidet die Parabel p: y=(x-2)² bei x=0
und berührt sie bei x=2.
Die beiden Parabeln schliessen im
1. Quadranten eine Fläche vom Inhalt A=4 ein. Bestimme
die Gleichung der Parabel 3. Ordnung. 

Stimmt.

Answer 2

du gehst das gut an, es fehlt nur noch etwas:
"Berührung" ist eine Angabe im Doppelpack: q´(2)=p´(2), das verwendest du ja auch, aber zusätzlich q(2)=p(2), das ist dir anscheinend durchgegangen.

Mit der Angabe kommst du sicher zu einer Gleichung, das hast du beim anderen Schnittpunkt ja schon gezeigt.

Beim Integral hast du dann die Integrationsgrenzen nicht konkret eingetragen - das sind genau die beiden Schnittstellen (0 und 2, die waren ja in der Aufgabe schon angegeben)

Und dann musst du die Stammfunktion bilden - also "aufleiten". Die Differenz F(2)-F(0) setzt du dann einmal gleich 4 und dann noch einmal =-4. Es könnte demnach auf zwei verschiedene Lösungen rauslaufen.

Wenn du noch weitere Hinweise brauchst, gibt es hier mehr über Steckbriefaufgaben: (mathebaustelle).

Ich hoffe, das hilft dir weiter.

Answer 3

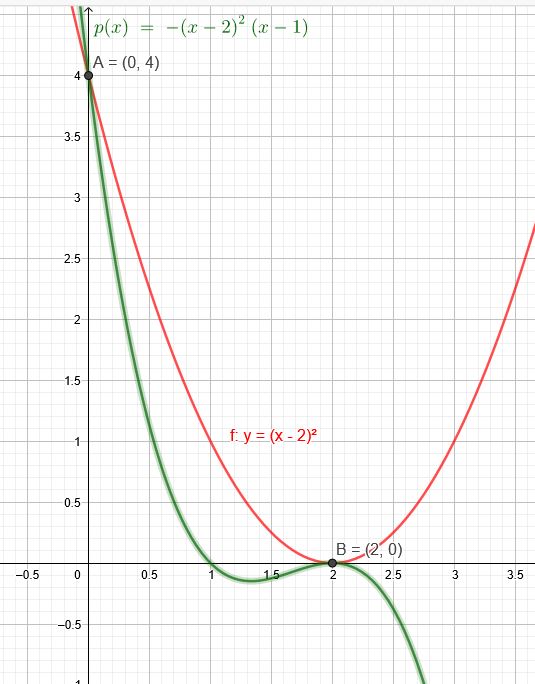
Eine Parabel 3. Ordnung schneidet die Parabel p: \(y=(x-2)^{2}\) bei \(x=0\) und berührt sie bei \(x=2\). Die beiden Parabeln schließen im 1. Quadranten eine Fläche vom Inhalt \(A=4\) ein. Bestimme die Gleichung der Parabel 3. Ordnung.

\(f(x)=(x-2)^{2}\) Schnitt  bei \(x=0\) :\(y=4\)   Y \((0|4)\)

berührt sie bei \(x=2\)  ist bei \(y=0\)  Somit doppelte Nullstelle.

\(p(x)=a(x-2)^2(x-N)\)

Y \((0|4)\):

\(p(0)=a(0-2)^2(0-N)=-4aN=4\)

\(a=-\frac{1}{N}\)

\(p(x)=-\frac{1}{N}(x-2)^2(x-N)\)

Die beiden Parabeln schließen im 1. Quadranten eine Fläche vom Inhalt \(A=4\) ein.

Differenzfunktion:

\(d(x)=p(x)-f(x)\)

\(d(x)=-\frac{1}{N}(x-2)^2(x-N)-(x-2)^{2}\)

\(d(x)=-\frac{1}{N}\red{[}(x-2)^2[x-N-1]\red{]}\)

\(d(x)=-\frac{1}{N}\red{[}x^3-5x^2-Nx^2+8x+4Nx-4N-4\red{]}\)

\( 4=\int\limits_{0}^{2}(- \frac{1}{N})\red{[}x^3-5x^2-Nx^2+8x+4Nx-4N-4\red{]}\)

\( -4N=\int\limits_{0}^{2}\red{[}x^3-5x^2-Nx^2+8x+4Nx-4N-4\red{]}\\=[\frac{1}{4}x^4-\frac{5}{3}x^3-\frac{N}{3}x^3+4x^2+2Nx^2-4Nx-4x]_{0}^{2}\\=[4-\frac{40}{3}-\frac{8N}{3}+16+8N-8N-8]-[0]\\=[-\frac{4}{3}-\frac{8N}{3}]\)

\(N=1\)  \(a=-1\)

\(p(x)=-(x-2)^2(x-1)\)

Rechnung mit Vorbehalt! ( Ich bin mir nicht sicher, ob die Fläche im 4. Quadranten noch abgezogen werden muss.)