Moinsen!
Wir haben Aufgabenteil 1.1 und 1.2 bearbeitet ;) und können uns darauf aufbauend ein Bild machen, wie wir Aufgabenteil 1.3 lösen könnten:
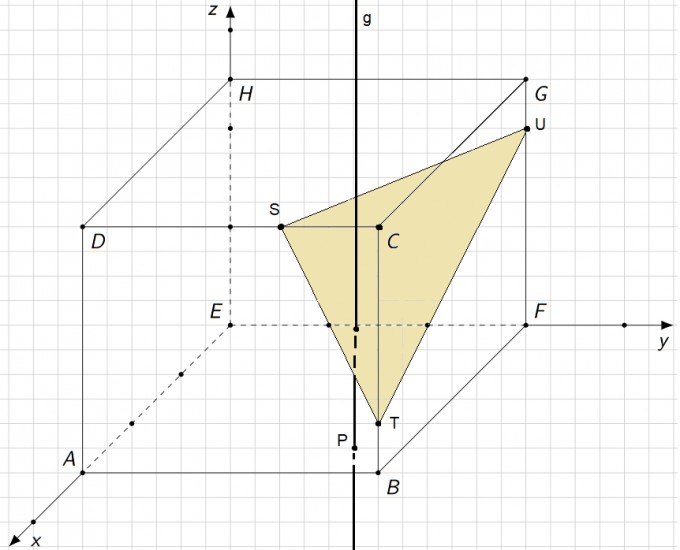
Geradengleichung der Geraden \( g: \vec{x} = \begin{pmatrix}x \\y \\z \end{pmatrix} = \begin{pmatrix}2,5 \\2,5 \\0 \end{pmatrix} + t \begin{pmatrix}0 \\0 \\ 1\end{pmatrix} \)
Gleichug der Ebene \(E: x + 4y + 2z = 16 \)
Gesucht: \(z\)-Koordinate des Schnittpunktes der Geraden mit der Ebene.
Aus der Geradengleichung bekommen wir die Koordinaten der Geraden in Parameterform:
\(x = 2.5 + t\cdot 0 = 2.5 \)
\(y = 2.5 + t\cdot 0 = 2.5 \)
\(z = 0 + t\cdot 1 = t \)
Ein Punkt der Geraden liegt in der Ebene, wir setzen \(x, y, z \) in die Ebenengleichung ein
\(2.5 + 4 \cdot 2,5 + 2 \cdot t = 16 \) und lösen nach \(t \) auf: \(t = 1,75 \).
\(t = 1,75 \) setzen wir in die Geradengleichung ein
\(\vec{x} = \begin{pmatrix}x \\y \\z \end{pmatrix} = \begin{pmatrix}2,5 \\2,5 \\0 \end{pmatrix} + 1,75\begin{pmatrix}0 \\0 \\1 \end{pmatrix}\) und bekommen
\(z = 1,75\)
Grüße