Hallo
Ansatz:$$f(x) = ax^3 + bx^2 + cx + d \\ \\f(-2) = -7\\-8a + 4b -2c + d = -7\\f(-1) = -4\\-a + b - c + d = -4\\f(0) = -1\\ax^3 + bx^2 + cx + d = -1\\d = -1\\f(1) = 0\\a + b + c + d = 0\\f(2) = 5\\8a + 4b + 2c + d = 5\\$$
$$Ax = b \\ \begin{pmatrix} -8& 4 & -2 & 1\\ -1& 1 & -1 & 1\\0 &0 &0 &1 \\1 & 1 &1 &1\\8 & 4 &2 &1\end{pmatrix} \begin{pmatrix}a\\b\\c\\d\end{pmatrix} = \begin{pmatrix}-7\\-4\\-1\\0\\5\end{pmatrix} \\A^TAx = A^Tb \\\begin{pmatrix} -8&-1 & 0 &1&8\\4 & 1 & 0&1&4\\-2 & -1 & 0&1&2\\1 & 1 & 1&1&1\end{pmatrix} \begin{pmatrix} -8& 4 & -2 & 1\\ -1& 1 & -1 & 1\\0 &0 &0 &1 \\1 & 1 &1 &1\\8 & 4 &2 &1\end{pmatrix} \begin{pmatrix}a\\b\\c\\d\end{pmatrix} = \begin{pmatrix} -8&-1 & 0 &1&8\\4 & 1 & 0&1&4\\-2 & -1 & 0&1&2\\1 & 1 & 1&1&1\end{pmatrix}\begin{pmatrix}-7\\-4\\-1\\0\\5\end{pmatrix} \\\begin{pmatrix}130 & 0 &34&0 \\0 & 34&0&10 \\34 &0 &10&0\\0 &10 &0&5 \end{pmatrix} \begin{pmatrix}a\\b\\c\\d\end{pmatrix} = \begin{pmatrix} 100\\-12 \\28 \\-7 \end{pmatrix} \\\Rightarrow LGS \\\Rightarrow \\130a + 34c = 100 \\34b + 10d = -12 \\34a + 10c = 28 \\10b + 5d = -7 \\\Rightarrow \\a = \frac{1}{3}, \ b=\frac{1}{7}, \ c = \frac{5}{3}, \ d=-\frac{59}{35}$$ $$f(x) = \frac{1}{3}x^3 + \frac{1}{7}x^2 + \frac{5}{3}x - \frac{59}{35}$$
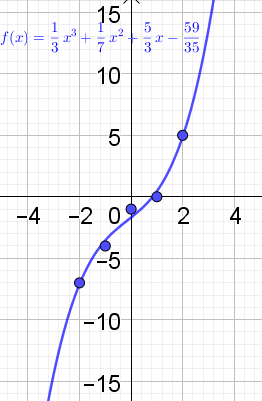
Grüße