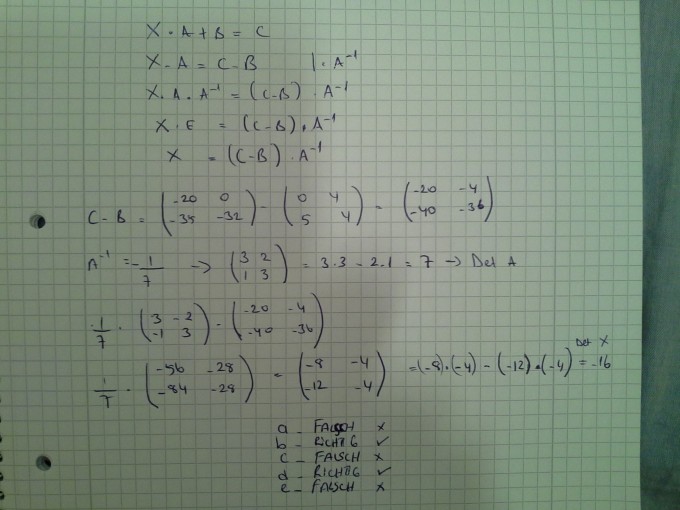Gegeben sei die Matrixgleichung X*A+B=C mit den Matrizen
A:(3 2; 1 3)
B:(0 4; 5 4)
C:(-20 0; -35 -32)
Bestimmen sie die Matrix X und kreuzen Sie allerichtigen Antworten an.
a - x12 < -9
b- die Determinante der Matrix A ist 7
c- x11>-7
d- die Determinante der Matrix X ist -6
e-x22 = -1
Und meine Antwort