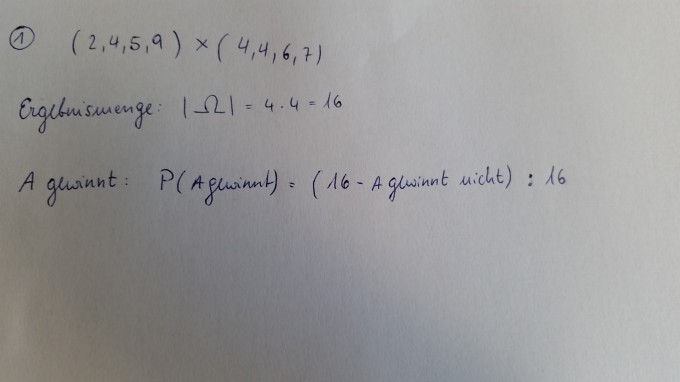Würfel A und B. Mit welcher Wahrscheinlichkeit gewinnt A?

Question

bräuchte bitte hilfe. mein ansatz steht unten. vielen dank!

Man betrachte zwei vierseitige Würfel. Der erste Würfel A hat die Ziffern 2,4,5,9 aufgedruckt, der zweite Würfel B hat die Ziffern 4,4,6,7 aufgedruckt.
Mit welcher Wahrscheinlichkeit gewinnt A, wenn beide Würfel einmal geworfen werden und die höhere Augenzahl gewinnt?

mir fehlt nur, wann A nicht gewinnt...

  

Answer 1

Schreib dir doch mal die 16 möglichen, nicht notwendig verschiedenen, Paare auf...

Comments

A verliert bei 2; 4; 5 ?

---

Bei (5,4) gewinnt A...

---

danke für die antwort. also folgt daraus dass A in 3 Ergebnissen verliert?

---

Nein, das folgt daraus nicht. Und warum interessiert es dich, wann A verliert? Das macht es doch hier nicht einfacher. Schreib die 16 möglichen Paare auf und markiere die Paare, bei denen A gewinnt.

---

damit ich es in die formel einsetzen kann. ok werde ich machen

---

Welche Formel?

Hier mal ein möglicher Ansatz über eine Tabelle:

$$ \begin{pmatrix}  {_A}{^B} & 4 & 4 & 6 & 7\\ 2 & - &  &  &  \\ 4 & - &  &  &  \\ 5 & + & + & - & - \\ 9 & + &  &  &  \\ \end{pmatrix} $$\(+\) bedeutet, dass A gewinnt, \(-\) dass A nicht gewinnt und wo nix steht, muss die Tabelle noch ergänzt werden.

---

vielen dank für die tabelle! mit der formel meinte ich "(16- A(gewinnt nicht) :16)"

deshalb wollte ich wissen in welchen Ergebnissen A nicht gewinnt

---

0.125 +0.125 +0.0625 +0.0625 = 0.375

kann das stimmen?

---

Ja, einfaches Auszählen ergibt 6/16=3/8=0.375 als Wahrscheinlichkeit dafür, dass A gewinnt. Deine Rechnung erscheint unnötig kompliziert, aber das Ergebnis stimmt.