vektor berechnen durch winkel

Question

ein Vektor a schließt mit des x- Achse den Winkel alpha=60 grad, mit der z-Achse den Winkel Beta=135grad und mit der y-Achse einen stumpfen Winkel ein; Seine Länge ist 4;

wie lautet der vektor a?

Danke

Answer 1

a = (x,y,z) und |a| = 4 

x = a*(1;0;0) =|a|*1*cos(60°) = 4*cos(60°) = 0,5

z= a*(0;0;1) = 4*cos(135° ) = -2√2 

==>   a =  ( 0,5 ;  y ;  -2√2  )  

und mit |a| = 4 ==>   4 = √ ( 0,25 + y^2 + 8 )

                      ==>   16 = 8,25+y^2 

                     ==>  y = ±√7,75

                 Und wegen des stumpfen Winkels ist die

negative Lösung die richtige.

Answer 2

Allgemein lässt sich für jeden Vektor \(\vec{v}\) der Länge \(l\) in einem dreidimensionalen Koordinatensystem schreiben

$$\vec{v}=l \cdot \frac{\vec{v}}{l}= l\cdot \begin{pmatrix} \cos{(\angle v,x)} \\ \cos{(\angle v,y)}\\ \cos(\angle v,z) \end{pmatrix}$$

Hier ist:

$$\cos(\angle v,x) = \cos(60°)=\frac12$$

$$\cos(\angle v,z) = \cos(135°)= -\frac12 \sqrt{2}$$

und ganz allgemein gilt

$$\cos^2(\angle v,x) + \cos^2(\angle v,y) + \cos^2(\angle v,z)= 1$$

also

$$\cos(\angle v,y) = \pm \sqrt{1 - \cos^2(\angle v,x) - \cos^2(\angle v,z)}= \pm \sqrt{1-\frac14 - \frac12} = \pm \frac12$$

Und da es sich bei \(\angle(v,y)\) um einen stumpfen Winkel handelt, muss sein Cosinus kleiner 0 sein. Demnach ist \(\vec{v}\)

$$\vec{v}= 4 \cdot \begin{pmatrix} \frac12\\ -\frac12\\ -\frac12\sqrt{2}\end{pmatrix} = \begin{pmatrix} 2\\ -2\\ -2\sqrt{2}\end{pmatrix}$$

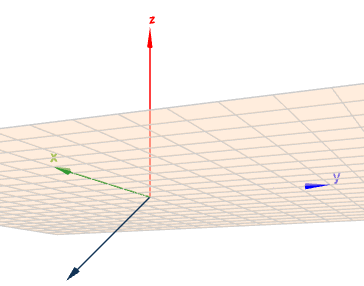
(klick mich)