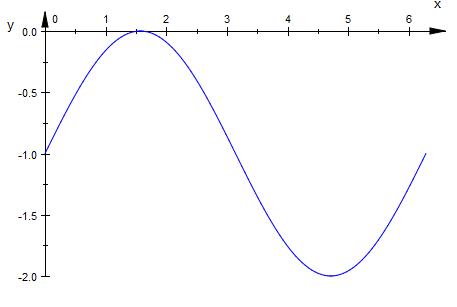
f ( x ) = a * sin ( b * x ) + d
f ´( x ) = a * cos ( b * x ) * b
f ( π / 2 ) = a * sin ( b * π / 2 ) + d = 0
f ( (3π) / 2 ) = a * sin ( b * (3π) / 2 ) + d = -2
f ´ ( π / 2 ) = a * cos ( b * π / 2 ) * b = 0
f ´ ( (3π) / 2 ) = a * cos ( b * (3π) / 2 ) * b = 0
Satz vom Nullprodukt anwenden
a ≠ 0
b ≠ 0
cos ( b * π / 2 ) = 0
cos ( b * (3π) / 2 ) = 0
Allgemein für die cos Funktion gilt
cos ( π / 2 ) = 0
cos ( π / 2 ) = cos ( b * π / 2 )
π / 2 = b * π / 2
b = 1
a * sin ( b * π / 2 ) + d = 0
a * sin ( b * (3π) / 2 ) + d = -2
a * sin ( π / 2 ) + d = 0
a * sin ( (3π) / 2 ) + d = -2
a * 1 + d = 0
a * (-1) + d = -2
a = - d
-d * (-1) + d = -2
2d = -2
d = -1
a = 1
f ( x ) = 1 * sin ( 1 * x ) -1