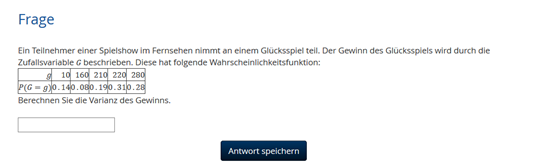
Ein Teilnehmer einer Spielshow im Fernsehen nimmt an einem Glücksspiel teil. Der
Gewinn des Glücksspiels wird durch die Zufallsvariable G beschrieben. Diese hat
folgende Wahrscheinlichkeitsfunktion:
g 10 160 210 220 280
P(G=g) 0.14 0.08 0.19 0.31 0.28
Berechnen sie die Varianz.
Mein Ansatz würde so lauten:
V(x)=10^2*0.14*160^2*0.08+210^2*0.19+220^2*0.31+280^2*0.28-200.7^2
Das Ergebnis bzw. die Varianz wäre somit 7116.52.
Wäre dieses Ergebnis richtig?:)